题目内容
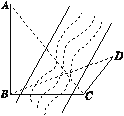
【题目】如图，为测得河对岸塔AB的高，先在河岸上选一点C，使C在塔底B的正东方向上，测得点A的仰角为60°，再由点C沿北偏东15°方向走10 m到位置D，测得∠BDC＝45°，则塔AB的高是（ ）
A. 10m B. 10
m C. 10
m D. 10
m
【答案】D
【解析】试题分析：先在△ABC中求出BC，再△BCD中利用正弦定理，即可求得结论．
解：设塔高AB为x米，根据题意可知在△ABC中，∠ABC=90°，∠ACB=60°，AB=x，从而有BC=
x，AC=
x
在△BCD中，CD=10，∠BCD=60°+30°+15°=105°，∠BDC=45°，∠CBD=30°
由正弦定理可得，
=
∴BC=
=10
∴
x=10
∴x=
故塔高AB=
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为了参加第二届全国数学建模竞赛，长郡中学在高二年级举办了一次选拔赛，共有60名高二学生报名参加，按照不同班级统计参赛人数，如表所示：
班级 | 宏志班 | 珍珠班 | 英才班 | 精英班 |
参赛人数 | 20 | 15 | 15 | 10 |
（Ⅰ）从这60名高二学生中随机选出2人，求这2人在同一班级的概率；
（Ⅱ）现从这60名高二学生中随机选出2人作为代表，进行大赛前的发言，设选出的2人中宏志班的学生人数为
，求随机变量
的分布列和数学期望．
