题目内容
3.已知函数f(x)=2cosxsin(x+$\frac{π}{6}$)+1,x∈R.(1)求函数f(x)的最小正周期及在[0,π]上的单调递增区间;
(2)若x∈[-$\frac{π}{6}$,$\frac{π}{3}$],求函数的值域.
分析 (1)展开两角和的正弦,再用降幂公式及辅助角公式化简,周期可求,再由复合函数的单调性求得函数f(x)在[0,π]上的单调递增区间;
(2)直接由x的范围求得相位的范围,进一步求得函数的值域.
解答 解:(1)∵f(x)=2cosxsin(x+$\frac{π}{6}$)+1=2cosx(sinxcos$\frac{π}{6}$+cosxsin$\frac{π}{6}$)+1
=$\frac{\sqrt{3}}{2}sin2x+co{s}^{2}x+1$=$\frac{\sqrt{3}}{2}sin2x+\frac{1}{2}cos2x+\frac{3}{2}$=$sin(2x+\frac{π}{6})+\frac{3}{2}$.
∴T=π,
由$-\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{π}{2}+2kπ$,得$-\frac{π}{3}+kπ≤x≤\frac{π}{6}+kπ,k∈Z$.
∴当k=0和k=1时,得到函数f(x)在[0,π]上的单调递增区间为$[{0,\frac{π}{6}}]$和$[{\frac{2π}{3},π}]$;
(2)由x∈[-$\frac{π}{6}$,$\frac{π}{3}$],得$2x+\frac{π}{6}∈[-\frac{π}{6},\frac{5π}{6}]$,
∴函数的值域为$[{1,\frac{5}{2}}]$.
点评 本题考查正弦函数的图象和性质,考查了三角恒等变换及其应用,考查了三角函数的化简求值,是中档题.

练习册系列答案
相关题目
13.已知命题p:$?x∈[\frac{1}{2},2],{x^2}-2x+2-a≥0$,命题q:?x∈R,x2-2ax+2-a=0,若命题“p∧q”是真命题,则实数a的取值范围是( )
| A. | (-∞,-2]∪{1} | B. | (-∞,-2]∪[1,2] | C. | [1,+∞) | D. | [-2,1] |
18.已知$\overrightarrow a=({1,-3})$,$\overrightarrow b=({3,2sinα})$,若$\overrightarrow a⊥\overrightarrow b$,则$cos({\frac{π}{2}+α})$=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
12.已知l是圆O:x2+y2=2的切线,1与椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1交于A,B两点,则△AOB面积的最大值为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{3\sqrt{2}}{2}$ | D. | 2$\sqrt{2}$ |
13.若C${\;}_{n}^{2}$=C${\;}_{n-1}^{2}$+C${\;}_{n-1}^{3}$(n∈N*),则($\root{3}{x}$-$\frac{1}{2\sqrt{x}}$)n的常数项为( )
| A. | -6 | B. | 12 | C. | $\frac{5}{2}$ | D. | -$\frac{5}{2}$ |
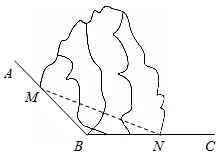 如图所示,AB,BC是两条傍山公路,∠ABC=120°,现在拟从M,N两处修建一条隧道(单位:千米).
如图所示,AB,BC是两条傍山公路,∠ABC=120°,现在拟从M,N两处修建一条隧道(单位:千米).