题目内容
设α、β、γ∈(0,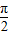 )且sinα+sinγ=sinβ,cosα+cosγ=cosβ,则α-β= .
)且sinα+sinγ=sinβ,cosα+cosγ=cosβ,则α-β= .
【答案】分析:依题意,利用sin2γ+cos2γ=1即可求得α-β.
解答:解:∵sinα+sinγ=sinβ,cosα+cosγ=cosβ,γ∈(0,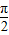 ),
),
∴sinγ=sinβ-sinα,
cosγ=cosβ-cosα>0,
∴cosβ>cosα,故0<β<α<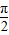 ,
,
∴α-β>0;①
∵sin2γ+cos2γ=(sinβ-sinα)2+(cosβ-cosα)2=1,
即2-2sinβsinα-2cosβcosα=1,
∴cos(α-β)= ;
;
∵α、β∈(0,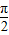 ),
),
∴-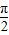 <α-β<
<α-β<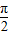 ②
②
由①②得0<α-β<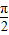 ,
,
∴α-β=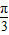 .
.
故答案为: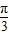 .
.
点评:本题考查两角和与差的余弦函数,由sin2γ+cos2γ=1作为突破口是关键,属于中档题.
解答:解:∵sinα+sinγ=sinβ,cosα+cosγ=cosβ,γ∈(0,
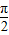 ),
),∴sinγ=sinβ-sinα,
cosγ=cosβ-cosα>0,
∴cosβ>cosα,故0<β<α<
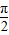 ,
,∴α-β>0;①
∵sin2γ+cos2γ=(sinβ-sinα)2+(cosβ-cosα)2=1,
即2-2sinβsinα-2cosβcosα=1,
∴cos(α-β)=
 ;
;∵α、β∈(0,
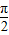 ),
),∴-
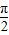 <α-β<
<α-β<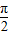 ②
②由①②得0<α-β<
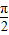 ,
,∴α-β=
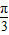 .
.故答案为:
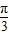 .
.点评:本题考查两角和与差的余弦函数,由sin2γ+cos2γ=1作为突破口是关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
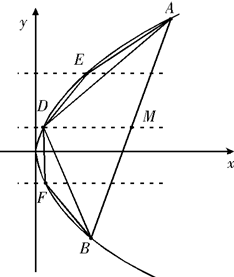 (2007•浦东新区二模)已知抛物线C:y2=2px(p>0)上横坐标为4的点到焦点的距离为5.
(2007•浦东新区二模)已知抛物线C:y2=2px(p>0)上横坐标为4的点到焦点的距离为5.