题目内容
对于区间[m,n]上有意义的两个函数f(x)与g(x),如果对任意x∈[m,n]
均有|f(x)﹣g(x)|≤1,则称f(x)与g(x)在[m,n]上是接近的;否则,称f(x)与g(x)在[m,n]上是非接近的.现有两个函数f1(x)=loga(x﹣3a)与 (a>0且a≠1),f1(x)与f2(x)在给定区间[a+2,a+3]上都有意义,
(a>0且a≠1),f1(x)与f2(x)在给定区间[a+2,a+3]上都有意义,
(1)求a的取值范围;
(2)问f1(x)与f2(x)在给定区间[a+2,a+3]上是否为接近的?请说明理由.
均有|f(x)﹣g(x)|≤1,则称f(x)与g(x)在[m,n]上是接近的;否则,称f(x)与g(x)在[m,n]上是非接近的.现有两个函数f1(x)=loga(x﹣3a)与
 (a>0且a≠1),f1(x)与f2(x)在给定区间[a+2,a+3]上都有意义,
(a>0且a≠1),f1(x)与f2(x)在给定区间[a+2,a+3]上都有意义,(1)求a的取值范围;
(2)问f1(x)与f2(x)在给定区间[a+2,a+3]上是否为接近的?请说明理由.
解:(1)要使f1(x)与f2(x)有意义,
则有
要使f1(x)与f2(x)在给定区间[a+2,a+3]上都有意义,
等价于: 所以0<a<1.
所以0<a<1.
(2)f1(x)与f2(x)在给定区间[a+2,a+3]上是接近的,
 对
对
于任意x∈[a+2,a+3]恒成立.
设h(x)=(x﹣2a)2﹣a2,x∈[a+2,a+3],
且其对称轴x=2a<2在区间[a+2,a+3]的左边


所以,当 时,f1(x)与f2(x)在给定区间[a+2,a+3]上是接近的;
时,f1(x)与f2(x)在给定区间[a+2,a+3]上是接近的;
当 时,f1(x)与f2(x)在给定区间[a+2,a+3]上是非接近的.
时,f1(x)与f2(x)在给定区间[a+2,a+3]上是非接近的.
则有

要使f1(x)与f2(x)在给定区间[a+2,a+3]上都有意义,
等价于:
 所以0<a<1.
所以0<a<1.(2)f1(x)与f2(x)在给定区间[a+2,a+3]上是接近的,
 对
对
于任意x∈[a+2,a+3]恒成立.
设h(x)=(x﹣2a)2﹣a2,x∈[a+2,a+3],
且其对称轴x=2a<2在区间[a+2,a+3]的左边



所以,当
 时,f1(x)与f2(x)在给定区间[a+2,a+3]上是接近的;
时,f1(x)与f2(x)在给定区间[a+2,a+3]上是接近的;当
 时,f1(x)与f2(x)在给定区间[a+2,a+3]上是非接近的.
时,f1(x)与f2(x)在给定区间[a+2,a+3]上是非接近的.
练习册系列答案
相关题目
 (a>0,a≠1)
(a>0,a≠1)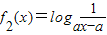 (a>0且a≠1),f1(x)与f2(x)在给定区间[a+2,a+3]上都有意义,
(a>0且a≠1),f1(x)与f2(x)在给定区间[a+2,a+3]上都有意义,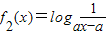 (a>0且a≠1),f1(x)与f2(x)在给定区间[a+2,a+3]上都有意义,
(a>0且a≠1),f1(x)与f2(x)在给定区间[a+2,a+3]上都有意义,