题目内容
已知抛物线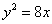 的准线与x轴交于点Q.
的准线与x轴交于点Q.
(1)若过点Q的直线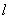 与抛物线有公共点,求直线
与抛物线有公共点,求直线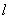 的斜率的取值范围;
的斜率的取值范围;
(2)若过点Q的直线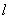 与抛物线交于不同的两点A、B,求AB中点P的轨迹方程。
与抛物线交于不同的两点A、B,求AB中点P的轨迹方程。
【答案】
解:(1)抛物线的准线为 ,点Q坐标为
,点Q坐标为
显然 的斜率存在,设为k,则直线
的斜率存在,设为k,则直线 的方程为:
的方程为:
联立: 化简得:
化简得: (1)
(1)
直线 与抛物线有公共点,即方程(1)有非负实根。
与抛物线有公共点,即方程(1)有非负实根。
当 时,
时,
当 时,
时, ,得:
,得: 且
且
综上知,直线 的斜率k的取值范围为
的斜率k的取值范围为
(2)由(1)知,当 时,直线
时,直线 与抛物线交于不同的两点。
与抛物线交于不同的两点。
设 ,设AB中点
,设AB中点
由(1) ,
, ,
,
由中点坐标公式:
消去参数k得:

练习册系列答案
相关题目
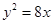 的准线与x轴交于点Q.
的准线与x轴交于点Q. 与抛物线有公共点,求直线
与抛物线有公共点,求直线