题目内容
在正四面体ABCD的面上，到棱AB以及C、D两点的距离都相等的点共有（ ）
分析：先找出到C、D两点的距离都相等的点满足的条件，再找出到棱AB、CD的距离相等的点满足的条件，则其交线上的任意一点满足到棱AB以及C、D两点的距离都相等．
解答：解：如图所示：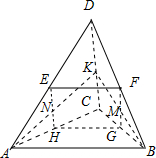
取CD的中点K，连接AK、BK，∵AK⊥CD，BK⊥CD，∴C、D两点关于平面ABK对称，
则平面ABK上的任意一点到C、D两点的距离都相等．
分别取棱AD、AC、BC、BD的中点E、H、G、F，连接EF、FG、GH、HE，则四边形EFGH是矩形，此矩形满足到棱AB、CD的距离相等．设EH∩AK=N，FG∩BK=M．由于AN=NK，BM=MK，则点M、N满足到棱AB以及C、D两点的距离都相等．
只有M、N两点满足条件，故答案为B．
故选B．
取CD的中点K，连接AK、BK，∵AK⊥CD，BK⊥CD，∴C、D两点关于平面ABK对称，
则平面ABK上的任意一点到C、D两点的距离都相等．
分别取棱AD、AC、BC、BD的中点E、H、G、F，连接EF、FG、GH、HE，则四边形EFGH是矩形，此矩形满足到棱AB、CD的距离相等．设EH∩AK=N，FG∩BK=M．由于AN=NK，BM=MK，则点M、N满足到棱AB以及C、D两点的距离都相等．
只有M、N两点满足条件，故答案为B．
故选B．
点评：利用“交轨法”即可求出满足条件的点是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的，现投掷骰子根据其点数决定棋子是否移动：若投出的点数是偶数，棋子移动到另一个顶点；若投出的点数是奇数，则棋子不动．若棋子的初始位置在顶点A．
设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的，现投掷骰子根据其点数决定棋子是否移动：若投出的点数是偶数，棋子移动到另一个顶点；若投出的点数是奇数，则棋子不动.若棋子的初始位置在顶点A.
.求
设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的，现投掷骰子根据其点数决定棋子是否移动：若投出的点数是偶数，棋子移动到另一个顶点；若投出的点数是奇数，则棋子不动.若棋子的初始位置在顶点A.
.求