题目内容
已知函数 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若函数 的图像在点
的图像在点 处的切线的倾斜角为
处的切线的倾斜角为 ,问:
,问: 在什么范围取值时,对于任意的
在什么范围取值时,对于任意的 ,函数
,函数 在区间
在区间 上总存在极值?
上总存在极值?
(Ⅲ)当 时,设函数
时,设函数 ,若在区间
,若在区间 上至少存在一个
上至少存在一个 ,
,
使得 成立,试求实数
成立,试求实数 的取值范围.
的取值范围.
【答案】
解:(Ι)由 知:
知:
当 时,函数
时,函数 的单调增区间是
的单调增区间是 ,单调减区间是
,单调减区间是 ;
;
当 时,函数
时,函数 的单调增区间是
的单调增区间是 ,单调减区间是
,单调减区间是 ;………………4分
;………………4分
(Ⅱ)由
 ,
,
∴ ,
, .
………………………6分
.
………………………6分
故 ,
,
∴ ,
,
∵ 函数 在区间
在区间 上总存在极值,
上总存在极值,
∴ 有两个不等实根且至少有一个在区间
有两个不等实根且至少有一个在区间 内…………7分
内…………7分
又∵函数 是开口向上的二次函数,且
是开口向上的二次函数,且 ,∴
,∴  …………8分
…………8分
由 ,∵
,∵
 在
在 上单调递减,所以
上单调递减,所以
 ;∴
;∴ ,由
,由 ,解得
,解得 ;
;
综上得: 所以当
所以当 在
在 内取值时,对于任意的
内取值时,对于任意的 ,函数
,函数
 在区间
在区间 上总存在极值。………………………9分
上总存在极值。………………………9分
(Ⅲ) 令
令 ,则
,则


 .
.
① 当 时,由
时,由 得
得 ,从而
,从而 ,
,
所以,在 上不存在
上不存在 使得
使得 ;…………………11分
;…………………11分
② 当 时,
时, ,
, ,
,

在 上恒成立,故
上恒成立,故 在
在 上单调递增。
上单调递增。
故只要 ,解得
,解得 综上所述,
综上所述,
 的取值范围是
的取值范围是
【解析】略

练习册系列答案
相关题目

 .
. 的单调递增区间;
的单调递增区间; ,函数
,函数 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围. 分)
分) .
.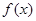 的最大值;
的最大值; 中,
中, ,角
,角 满足
满足 ,求
,求