题目内容
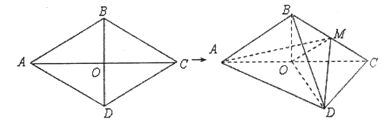
【题目】如图,棱形![]() 的边长为6,
的边长为6, ![]() ,
,![]() .将棱形
.将棱形![]() 沿对角线
沿对角线![]() 折起,得到三棱锥
折起,得到三棱锥![]() ,点
,点![]() 是棱
是棱![]() 的中点,
的中点, ![]() .
.
(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积.
的体积.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)求证:![]() 平面
平面![]() ,这是证明线面平行问题,证明线面平行,即证线线平行,可利用三角形的中位线,或平行四边形的对边平行,本题注意到
,这是证明线面平行问题,证明线面平行,即证线线平行,可利用三角形的中位线,或平行四边形的对边平行,本题注意到![]() 是
是![]() 的中点,点
的中点,点![]() 是棱
是棱![]() 的中点,因此由三角形的中位线可得,
的中点,因此由三角形的中位线可得,![]() ,从而可得
,从而可得![]() 平面
平面![]() ;(2)求三棱锥
;(2)求三棱锥![]() 的体积,由已知
的体积,由已知![]() ,由题意
,由题意![]() ,可得
,可得![]() ,从而得
,从而得![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() ,因此把求三棱锥
,因此把求三棱锥![]() 的体积,转化为求三棱锥
的体积,转化为求三棱锥![]() 的体积,因为高
的体积,因为高![]() ,求出
,求出![]() 的面积即可求出三棱锥
的面积即可求出三棱锥![]() 的体积.
的体积.
试题解析:(1)证明:因为点![]() 是菱形
是菱形![]() 的对角线的交点,
的对角线的交点,
所以![]() 是
是![]() 的中点.又点
的中点.又点![]() 是棱
是棱![]() 的中点,
的中点,
所以![]() 是
是![]() 的中位线,
的中位线,![]() . 2分
. 2分
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() , 4分
, 4分
所以![]() 平面
平面![]() . 6分
. 6分
(2)三棱锥![]() 的体积等于三棱锥
的体积等于三棱锥![]() 的体积. 7分
的体积. 7分
由题意,![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() . 8分
. 8分
又因为菱形![]() ,所以
,所以![]() . 9分
. 9分
因为![]() ,所以
,所以![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() 10分
10分
所以![]() 为三棱锥
为三棱锥![]() 的高. 11分
的高. 11分
![]() 的面积为
的面积为![]()
![]() , 13分
, 13分
所求体积等于![]()
![]() . 14分
. 14分

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目