题目内容
16．在△ABC中，∠A=30°，∠C=120°，$AB=6\sqrt{3}$，则AC的长为6．分析 利用已知及三角形内角和定理可求∠B，利用正弦定理即可求值得解．
解答 解：∵在△ABC中，∠A=30°，∠C=120°，
∴∠B=180°-∠A-∠C=30°，
∴由正弦定理可得：AC=$\frac{ABsinB}{sinC}$=$\frac{6\sqrt{3}×sin30°}{sin120°}$=6．
故答案为：6．
点评 本题主要考查了三角形内角和定理，正弦定理在解三角形中的应用，属于基础题．
练习册系列答案
名题金卷系列答案
优加精卷系列答案
相关题目
4．在等差数列{an}中，若a2=5，a10=21，则a6等于（ ）
| A． | 13 | B． | 15 | C． | 17 | D． | 48 |
11．设变量x，y满足约束条件$\left\{\begin{array}{l}2x+y≥4\\ x-y≤4\\ x-2y≥2\end{array}\right.$，则目标函数z=x+y-3的最小值为（ ）
| A． | -2 | B． | $-\frac{5}{3}$ | C． | -1 | D． | 5 |
1．（1）判断函数$f（x）=lnx-\frac{2}{x}$的零点个数；
（2）函数$g（x）=\frac{2}{x}+lnx+x-2-b（b∈R）$．在区间[e-1，e]上有两个零点，求实数b的取值范围；
（3）完成填空
（2）函数$g（x）=\frac{2}{x}+lnx+x-2-b（b∈R）$．在区间[e-1，e]上有两个零点，求实数b的取值范围；
（3）完成填空
| 用方程表述 | 用函数零点表述 | |
| 若函数y=f（x）和y=g（x）的图象在（a，b）内有交点 |
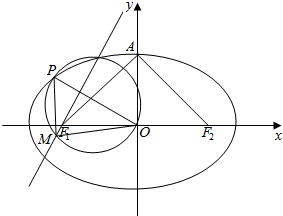如图，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点分别为F1，F2，点A是椭圆的上顶点，△AF1F2为等腰直角三角形，点P为椭圆任意一点，且|PF1|的最小值为$\sqrt{2}$-1；以OP为直径作圆E，过F1作OP的垂线交圆E于M．