题目内容
过原点O作圆x2+y2-2x-4y+4=0的任意割线交圆于P1,P2两点,求P1P2的中点P的轨迹.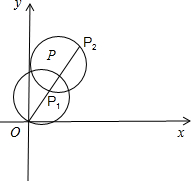
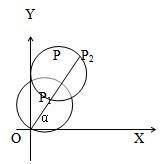
分析:设割线OP1P2的直线方程为y=kx与圆的方程联立得(1+k2)x2-2(1+2k)x+4=0,再由韦达定理得:x1+x2=
,因为P是P1P2的中点,所以x=
=
,再由P点在直线y=kx上,得到k=
,代入上式得x=
整理即可.要注意范围.
| 2(1+2k) |
| 1+k2 |
| x1+x2 |
| 2 |
| 1+2k |
| 1+k2 |
| y |
| x |
1+2
| ||
1+(
|
解答:解:设割线OP1P2的直线方程为y=kx代入圆的方程,
得:x2+k2x2-2x-4kx+4=0
即(1+k2)x2-2(1+2k)x+4=0
设两根为x1,x2即直线与圆的两交点的横坐标;
由韦达定理得:
x1+x2=
又设P点的坐标是(x,y)
P是P1P2的中点,所以x=
=
又P点在直线y=kx上,
∴k=
,代入上式得x=
两端乘以1+(
)2,得x+
=1+2
即x2+y2=x+2y
(x-
)2+(y-1)2=
这是一个一点(
,1)为中心,以
为半径的圆,
所求轨迹是这个圆在所给圆内的一段弧.
得:x2+k2x2-2x-4kx+4=0
即(1+k2)x2-2(1+2k)x+4=0
设两根为x1,x2即直线与圆的两交点的横坐标;
由韦达定理得:
x1+x2=
| 2(1+2k) |
| 1+k2 |
又设P点的坐标是(x,y)
P是P1P2的中点,所以x=
| x1+x2 |
| 2 |
| 1+2k |
| 1+k2 |
又P点在直线y=kx上,
∴k=
| y |
| x |
1+2
| ||
1+(
|
两端乘以1+(
| y |
| x |
| y2 |
| x |
| y |
| x |
即x2+y2=x+2y
(x-
| 1 |
| 2 |
| 5 |
| 4 |
这是一个一点(
| 1 |
| 2 |
| ||
| 2 |
所求轨迹是这个圆在所给圆内的一段弧.
点评:本题主要考查直线与圆的位置关系,韦达定理,中点坐标公式及点的轨迹方程.

练习册系列答案
相关题目
过原点O作圆x2+y2-8x=0的弦OA.
(1)求弦OA中点M的轨迹方程;
(2)如果M(x,y)是(1)中的轨迹上的动点,
①求T=x2+y2+4x-6y的最大、最小值;
②求N=
的最大、最小值.
(1)求弦OA中点M的轨迹方程;
(2)如果M(x,y)是(1)中的轨迹上的动点,
①求T=x2+y2+4x-6y的最大、最小值;
②求N=
| y | x+2 |
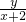 的最大、最小值.
的最大、最小值. 的最大、最小值.
的最大、最小值.