题目内容
如图,底面为直角梯形的四棱锥 中,AD∥BC,
中,AD∥BC,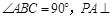 平面
平面 ,
, 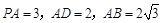 ,BC=6.
,BC=6.
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角 的余弦值.
的余弦值.
(Ⅰ)详见解析;(Ⅱ)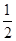
解析试题分析:本题主要以四棱锥为几何背景考察线面垂直和二面角的求法,可以用传统几何法,也可以用空间向量法,突出考察空间想象能力和计算能力,(Ⅰ)由 平面
平面 ,得到
,得到
 ,要证明
,要证明
 平面
平面 ,只需证明
,只需证明
 ,在
,在 中,
中,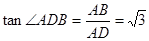 ,在
,在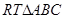 中,
中, ,所以
,所以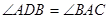 ,又
,又 ,
, ,所以
,所以
 ,可证
,可证
 平面
平面 ;(Ⅱ)用向量法求解,先求出面
;(Ⅱ)用向量法求解,先求出面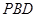 和面
和面 的法向量,再利用夹角公式求夹角.
的法向量,再利用夹角公式求夹角.
试题解析:(Ⅰ)方法一:如图,以A为坐标原点,建立如图所示空间直角坐标系,
则 ,
, ,
,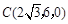 ,
,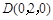 ,
, ,
,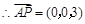 ,
,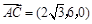 ,
, , 2分
, 2分 .
. ,
, ,
,
又 ,
,  面
面 . 6分
. 6分
方法二:由 平面
平面 ,∴
,∴
 ,在
,在 中,
中,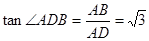 ,在
,在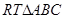 中,
中, ,所以
,所以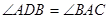 ,又
,又 ,
, ,所以
,所以
 ,又∵
,又∵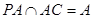 ,
, 面
面
(Ⅱ)设平面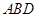 的法向量为
的法向量为 ,
,
设平面 的法向量为
的法向量为 ,
,
则 8分
8分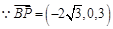
 解得.
解得.
令 ,则
,则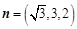 10分
10分
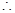 二面角
二面角 的余弦值为
的余弦值为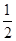 . 12分
. 12分
考点:1、线面垂直的判定定理;2、向量法求二面角的大小.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,侧面
中,侧面 与底面
与底面 垂直,
垂直,  分别是
分别是 的中点,
的中点,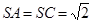 ,
,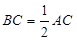 ,
,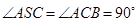 .
.
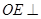 平面
平面 ;
; 为线段
为线段 的中点,求异面直线
的中点,求异面直线 与
与 所成角的正切值.
所成角的正切值.  .
.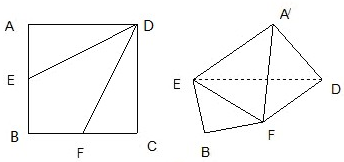
 ⊥EF;
⊥EF;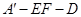 的平面角的余弦值.
的平面角的余弦值.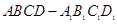 中,
中,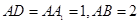 ,点E是AB的中点.
,点E是AB的中点.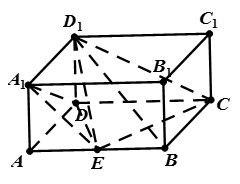
 平面
平面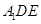 ;
;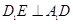 ;
;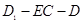 的正切值.
的正切值.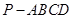 中,平面
中,平面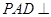 平面
平面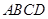 ,
,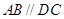 ,
,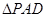 是等边三角形,已知
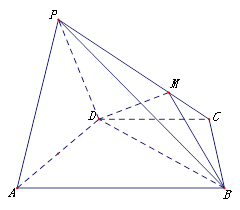
是等边三角形,已知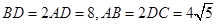 .
.
 是
是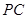 上的一点,证明:平面
上的一点,证明:平面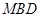 ;
;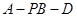 的余弦值.
的余弦值. ,?O的直径AB=2, C为弧AB的中点,D为AC的中点.
,?O的直径AB=2, C为弧AB的中点,D为AC的中点.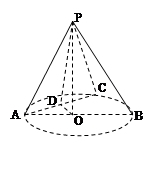
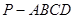 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱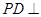 底面ABCD,
底面ABCD,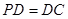 ,E是PC的中点.
,E是PC的中点.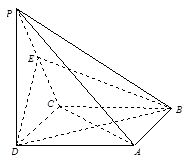
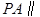 平面EDB;
平面EDB;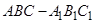 中,
中,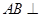 侧面
侧面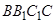 ,已知
,已知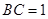 ,
,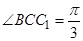 ,
,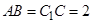 .
.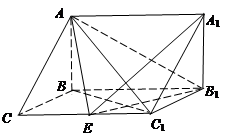
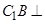 平面
平面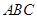 ;
;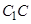 (不包含端点
(不包含端点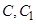 )上确定一点
)上确定一点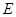 的位置,使得
的位置,使得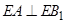 ;
;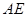 和平面
和平面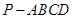 的底面为平行四边形,
的底面为平行四边形,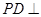 平面
平面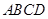 ,
,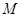 为
为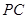 中点.
中点.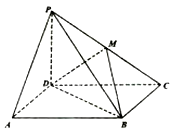
 平面
平面 ;
;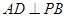 ,求证:
,求证: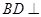 平面
平面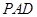 .
.