题目内容
若α∈(0,
),且cos2α+sin(
+2α)=
,则tanα=
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
1
1
.分析:由条件利用诱导公式、二倍角公式求得cos2α=
,cosα=
,α=
,从而求得 tanα 的值.
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
解答:解:∵α∈(0,
),且cos2α+sin(
+2α)=
,∴cos2α+cos2α=
,
即 3 cos2α=
,故 cos2α=
,
∴cosα=
,α=
,tanα=1,
故答案为 1.
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即 3 cos2α=
| 3 |
| 2 |
| 1 |
| 2 |
∴cosα=
| ||
| 2 |
| π |
| 4 |
故答案为 1.
点评:本题主要考查同角三角函数的基本关系,诱导公式、二倍角公式的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
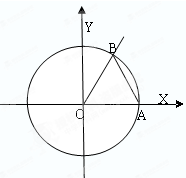 如图,在平面直角坐标系xoy中,角α的始边与x轴的非负半轴重合且与单位圆相交于A点,它的终边与单位圆相交于x轴上方一点B,始边不动,终边在运动.
如图,在平面直角坐标系xoy中,角α的始边与x轴的非负半轴重合且与单位圆相交于A点,它的终边与单位圆相交于x轴上方一点B,始边不动,终边在运动.