题目内容
用单调性的定义证明:函数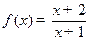 在
在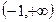 上是减函数。
上是减函数。
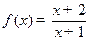 在
在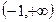 上是减函数。
上是减函数。证明略
设 是
是 上的任意两个实数,且
上的任意两个实数,且 ,
,
则
由 得
得 ,
, ;
;
由 得
得 ,
, .
.
于是 即
即 .
.

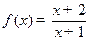 在
在 上是减函数。
上是减函数。
 是
是 上的任意两个实数,且
上的任意两个实数,且 ,
,则

由
 得
得 ,
, ;
;由
 得
得 ,
, .
.于是
 即
即 .
.
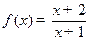 在
在 上是减函数。
上是减函数。
练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
题目内容
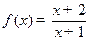 在
在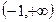 上是减函数。
上是减函数。 是
是 上的任意两个实数,且
上的任意两个实数,且 ,
,
 得
得 ,
, ;
; 得
得 ,
, .
. 即
即 .
.
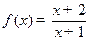 在
在 上是减函数。
上是减函数。
 金钥匙试卷系列答案
金钥匙试卷系列答案