题目内容
设数列{an}的前n项和为Sn,已知Sn+1=pSn+q(p,q为常数,n∈N*),a1=2,a2=1,a3=q-3p。
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)是否存在正整数m,n,使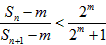 成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。
成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)是否存在正整数m,n,使
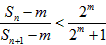 成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。
成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。 解:(Ⅰ)由题意,知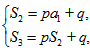 ,即
,即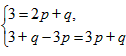 ,
,
解之得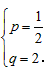 ,
,
由⑴知,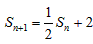 ,①
,①
当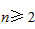 时,
时,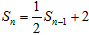 ,②
,②
①-②得,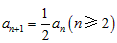 ,
,
又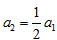 ,
,
所以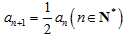 ,
,
所以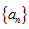 是首项为2,公比为
是首项为2,公比为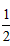 的等比数列,
的等比数列,
所以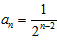 ;
;
(Ⅱ)由⑵得,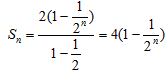 ,
,
由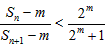 ,得
,得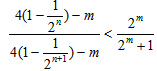 ,
,
即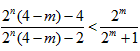 ,
,
即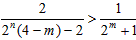 ,
,
因为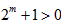 ,
,
所以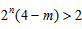 ,
,
所以m<4,
且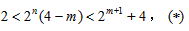
因为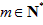 ,
,
所以m=1或2或3,
当m=1时,由(*)得,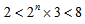 ,所以n=1;
,所以n=1;
当m=2时,由(*)得,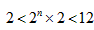 ,所以n=1或2;
,所以n=1或2;
当m=3时,由(*)得,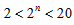 ,所以n=2或3或4,
,所以n=2或3或4,
综上可知,存在符合条件的所有有序实数对为: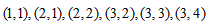 。
。

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目