题目内容
(本题满分12分)设Sn为数列{an}的前n项的和,且Sn =![]() (an -1)(n∈N*), 数列
(an -1)(n∈N*), 数列
{bn }的通项公式bn = 4n+5.
①求证:数列{an }是等比数列;
②若d∈{a1 ,a2 ,a3 ,……}∩{b1 ,b2 ,b3 ,……},则称d为数列{an }和{bn }的公共项,按它们在原数列中的先后顺序排成一个新的数列{dn },求数列{dn }的通项公式.
分析:①利用公式an=Sn-Sn-1代入得出an与an-1之间的关系.②令ak=bm ,再找出k,m之间的联系.
解:①当n=1时,由a1=S1=![]() ,得出a1=3.当n≥2时,
,得出a1=3.当n≥2时,![]() …………6分
…………6分
②由an=3n,得:
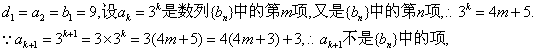
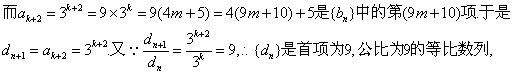
因此dn=9×9n—1、=9n. ……………………………………………………12分
评注:本题中的①,由Sn和Sn—1作两式相减,这是处理类似的关系式的重要的方法,特别是对于an+1=pan+q(p,q为常数)也是有效的.②的解法提供了一种求公共项的方法,若两个数列都是等差数列,则它们的公共项也为等差数列,公差为它们的最小公倍数.若都为等比数列,请读者思考公共项是否仍为等比数列

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 :实数
:实数 满足
满足 , 命题
, 命题 :实数
:实数 .
. 为真,求实数
为真,求实数 .
. 的单调区间;
的单调区间; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,其中
,其中 。
。 时,求不等式
时,求不等式 的解集;
的解集;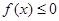 的解集为
的解集为 ,求a的值。
,求a的值。
 与
与 垂直,求
垂直,求 的值
的值  的最大值;
的最大值;  ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 与
与 、
、 两点,且
两点,且 ,
, ,
, 成等差数列,
成等差数列, 满足
满足 ,求
,求