题目内容
定义在区间(-1,1)上的函数f(x)满足:
①对任意x,y∈(-1,1),都有f(x)+f(y)=f(
);
②当x∈(-1,0)时,f(x)>0.求证:
(1)f(0)=0;
(2)f(x)在(-1,1)上是减函数;
(3)f(
)+f(
)+f(
)+…+f(
)>f(
).
①对任意x,y∈(-1,1),都有f(x)+f(y)=f(
| x+y |
| 1+xy |
②当x∈(-1,0)时,f(x)>0.求证:
(1)f(0)=0;
(2)f(x)在(-1,1)上是减函数;
(3)f(
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| 19 |
| 1 |
| n2+3n+1 |
| 1 |
| 2 |
分析:(1)令x=y=0,代入条件关系即可;
(2)令-1<x1<x2<1,然后构造f(x1)-f(x2),进而根据函数单调性的定义,进行判断即可;
(3)令y=-x,判断函数f(x)的奇偶性,可利用f(x)为奇函数,将要证f(
)+f(
)+f(
)+…+f(
)>f(
),转化为:也就是去证明-[f(
)+f(
)+f(
)+…+f(
)]<-f(
),即证明f(-
)+f(-
)+f(-
)+…+f(-
)<f(-
);而f(-
)=f(
)=f(n+2)-f(n+1),利用累加法,结合函数f(x)在(-1,1)上是减函数即可证明结论成立.
(2)令-1<x1<x2<1,然后构造f(x1)-f(x2),进而根据函数单调性的定义,进行判断即可;
(3)令y=-x,判断函数f(x)的奇偶性,可利用f(x)为奇函数,将要证f(
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| 19 |
| 1 |
| n2+3n+1 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| 19 |
| 1 |
| n2+3n+1 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| 19 |
| 1 |
| n2+3n+1 |
| 1 |
| 2 |
| 1 |
| n2+3n+1 |
| [(n+2)-(n+1)] |
| 1+(n+2)•[-(n+1)] |
解答:解:(1)令x=y=0,
有2f(0)=f(0),
∴f(0)=0;
(2)令-1<x1<x2<1,则
f(x1)-f(x2)=f(x1)+f(-x2)=f(
),
∵-1<x1<x2<1,
∴x1-x2<0,1-x1•x2>0,
∴-1<
<0,
∴f(
)>0,
即f(x1)>f(x2),
∴f(x)在(-1,1)上是减函数;
(3)令y=-x,则f(x)+f(-x)=f(0)=0,
∴f(-x)=-f(x),
∴f(x)为奇函数;
∴-f(
)=f(-
)=f(
) =f(3)+f(-2)=f(3)-f(2),①
-f(
)=f(-
)= =f(
) =f(4)+f(-3)=f(4)-f(3),②
…
-f(
)=f(-
)=f(n+2)+f[-(n+1)]=f(n+2)-f(n+1) ③
将上式①②…③n个式子累加有
-[f(
)+f(
)+f(
)+…+f(
)]
=f(-
)+f(-
)+f(-
)+…+f(-
)
=f(n+2)-f(2)=f(
),
又f(x)在(-1,1)上是减函数;
∴f(
)=f(-
)<f(-
) =-f(
)<f(-
) =-f(
),
∴f(
)+f(
)+f(
)+…+f(
)>f(
)
有2f(0)=f(0),
∴f(0)=0;
(2)令-1<x1<x2<1,则
f(x1)-f(x2)=f(x1)+f(-x2)=f(
| x1-x2 |
| 1-x1•x2 |
∵-1<x1<x2<1,
∴x1-x2<0,1-x1•x2>0,
∴-1<
| x1-x2 |
| 1-x1•x2 |
∴f(
| x1-x2 |
| 1-x1•x2 |
即f(x1)>f(x2),
∴f(x)在(-1,1)上是减函数;
(3)令y=-x,则f(x)+f(-x)=f(0)=0,
∴f(-x)=-f(x),
∴f(x)为奇函数;
∴-f(
| 1 |
| 5 |
| 1 |
| 5 |
| 3-2 |
| 1+3×(-2) |
-f(
| 1 |
| 11 |
| 1 |
| 11 |
| 4-3 |
| 1+4×(-3) |
…
-f(
| 1 |
| n2+3n+1 |
| (n+2)-(n-1) |
| 1+(n+2)•[-(n+1))] |
将上式①②…③n个式子累加有
-[f(
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| 19 |
| 1 |
| n2+3n+1 |
=f(-
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| 19 |
| 1 |
| n2+3n+1 |
=f(n+2)-f(2)=f(
| n |
| 1-2(n+2) |
又f(x)在(-1,1)上是减函数;
∴f(
| n |
| 1-2(n+2) |
| n |
| 2n+3) |
| n |
| 2n |
| 1 |
| 2 |
| n |
| 2n |
| 1 |
| 2 |
∴f(
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| 19 |
| 1 |
| n2+3n+1 |
| 1 |
| 2 |
点评:本题考查抽象函数及其应用,关键在于判断函数为奇函数后,灵活应用“对任意x,y∈(-1,1),都有f(x)+f(y)=f(
)”判断函数的单调性.属于难题.
| x+y |
| 1+xy |

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
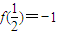 ,对任意x、y∈(-1,1),恒有
,对任意x、y∈(-1,1),恒有 成立,又数列an满足
成立,又数列an满足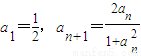 ,设
,设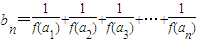 .
.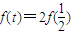 ;
;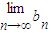 的值;
的值;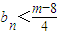 成立?若存在,求出m的最小值;若不存在,请说明理由.
成立?若存在,求出m的最小值;若不存在,请说明理由. ,对任意x、y∈(-1,1),恒有
,对任意x、y∈(-1,1),恒有 成立,又数列an满足
成立,又数列an满足 ,设
,设 .
. ;
; 的值;
的值; 成立?若存在,求出m的最小值;若不存在,请说明理由.
成立?若存在,求出m的最小值;若不存在,请说明理由.