题目内容
已知数列{an}的首项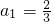 ,
, ,n=1,2,3,….
,n=1,2,3,….
(Ⅰ)证明:数列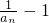 是等比数列;
是等比数列;
(Ⅱ)求数列 的前n项和Sn.
的前n项和Sn.
解:(Ⅰ)由已知: ,
,
∴ ,(2分)
,(2分)
∴ ,
,
又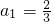 ,∴
,∴ ,(4分)
,(4分)
∴数列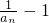 是以
是以 为首项,
为首项, 为公比的等比数列.(6分)
为公比的等比数列.(6分)
(Ⅱ)由(Ⅰ)知 ,
,
即 ,∴
,∴ .(8分)
.(8分)
设
 ,①
,①
则
 ,②
,②
由①-②得:
 ,(10分)
,(10分)
∴ .又1+2+3+
.又1+2+3+ .(12分)
.(12分)
∴数列 的前n项和:
的前n项和: .(14分)
.(14分)
分析:(1)化简 构造新的数列
构造新的数列 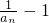 ,进而证明数列
,进而证明数列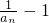 是等比数列.
是等比数列.
(2)根据(1)求出数列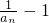 的递推公式,得出an,进而构造数列
的递推公式,得出an,进而构造数列 ,求出数列
,求出数列 的通项公式,进而求出前n项和Sn.
的通项公式,进而求出前n项和Sn.
点评:此题主要考查通过构造新数列达到求解数列的通项公式和前n项和的方法.
 ,
,∴
 ,(2分)
,(2分)∴
 ,
,又
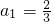 ,∴
,∴ ,(4分)
,(4分)∴数列
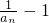 是以
是以 为首项,
为首项, 为公比的等比数列.(6分)
为公比的等比数列.(6分)(Ⅱ)由(Ⅰ)知
 ,
,即
 ,∴
,∴ .(8分)
.(8分)设

 ,①
,①则

 ,②
,②由①-②得:

 ,(10分)
,(10分)∴
 .又1+2+3+
.又1+2+3+ .(12分)
.(12分)∴数列
 的前n项和:
的前n项和: .(14分)
.(14分)分析:(1)化简
 构造新的数列
构造新的数列 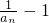 ,进而证明数列
,进而证明数列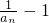 是等比数列.
是等比数列.(2)根据(1)求出数列
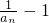 的递推公式,得出an,进而构造数列
的递推公式,得出an,进而构造数列 ,求出数列
,求出数列 的通项公式,进而求出前n项和Sn.
的通项公式,进而求出前n项和Sn.点评:此题主要考查通过构造新数列达到求解数列的通项公式和前n项和的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目