题目内容
20.(理) 曲线C:y=x3(x≥0)在点x=1处的切线为l,则由曲线C、直线l及x轴围成的封闭图形的面积是( )| A. | 1 | B. | $\frac{1}{12}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
分析 确定被积函数与被积区间,求出原函数,即可得到结论.
解答 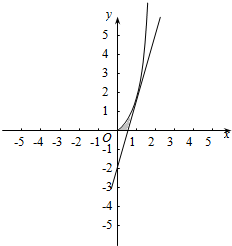 解:曲线C:y=x3(x≥0)的导数为y′=3x2,
解:曲线C:y=x3(x≥0)的导数为y′=3x2,
在点x=1处的切线斜率为3,切点为(1,1),
则切线的方程为y=3x-2,
y=3x-2与x轴的交点为$(\frac{2}{3},0)$,
所以由曲线C、直线l及x轴围成的封闭图形的面积是
S=${∫}_{0}^{1}$x3dx-${∫}_{\frac{2}{3}}^{1}$(3x-2)dx=$\frac{1}{4}$x4|${\;}_{0}^{1}$-($\frac{3}{2}$x2-2x)|${\;}_{\frac{2}{3}}^{1}$=$\frac{1}{4}$-$\frac{1}{6}$=$\frac{1}{12}$.
故选:B.
点评 本题考查面积的计算,解题的关键是确定曲线交点的坐标,确定被积区间及被积函数,利用定积分表示面积.

练习册系列答案
相关题目
8.$\frac{1-i}{{{{({1+i})}^2}}}$=( )
| A. | $\frac{1}{2}$+$\frac{i}{2}$ | B. | 1+$\frac{i}{2}$ | C. | -$\frac{1}{2}$-$\frac{i}{2}$ | D. | 1-$\frac{i}{2}$ |
15.“x>0”是“x2>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.已知集合A={-2,0,2},B={-1,2},则A∩B=( )
| A. | ∅ | B. | {2} | C. | {0} | D. | {-2} |
9.若f(x)=ex-ae-x为奇函数,则$f(x-1)<e-\frac{1}{e}$的解集为( )
| A. | (-∞,2) | B. | (一∞,1) | C. | (2,+∞) | D. | (1,+∞) |
10.已知集合A={x∈N+|$\frac{4}{x-4}$∈Z},则集合A中元素的个数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |