题目内容
设![]() ,函数
,函数![]() ,其中e是自然对数的底数。
,其中e是自然对数的底数。
(1)判断函数![]() 在R上的单调性;
在R上的单调性;
(2)当![]() 在[1,2]上的最小值。
在[1,2]上的最小值。
解:(1)![]()
由于![]() 只需讨论函数
只需讨论函数![]() 的符号:
的符号:
当a=0时,![]() ,即
,即![]() 上是减函数
上是减函数
当![]()
可知![]() 在R上是减函数;
在R上是减函数;
当a<0时,解![]()
在区间 上,
上,
![]() 函数
函数![]() 是增函数;
是增函数;
在区间 上,
上,
![]() 函数
函数![]() 是减函数;
是减函数;
综上可知:当![]() 时,函数
时,函数![]() 在R上是减函数;
在R上是减函数;
当a<0时,函数![]() 在区间
在区间 ;
;
在区间 上是减函数;在
上是减函数;在
区间 上是增函数;
上是增函数;
(2)当![]()
所以,函数![]() 上是减函数,
上是减函数,
其最小值是![]()

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 是定义在
是定义在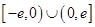 上的奇函数,当
上的奇函数,当 时,
时, 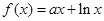 (其中e是自然对数的底,
(其中e是自然对数的底, 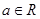 )
)
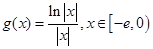 ,求证:当
,求证:当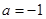 时,
时,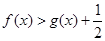 ;
; 时,
时, ,函数
,函数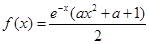 ,其中e是自然对数的底数。
,其中e是自然对数的底数。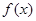 在[-1,2]上的最小值;
在[-1,2]上的最小值;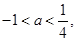 是否存在实数t,使得对于任意
是否存在实数t,使得对于任意 ,
,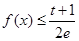 恒成立,存在,求出t的范围,不存在,说明理由。
恒成立,存在,求出t的范围,不存在,说明理由。 (其中e是自然对数的底数)
(其中e是自然对数的底数)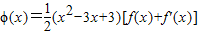 ,求证:对于任意的t>-2,总存在x∈(-2,t),满足
,求证:对于任意的t>-2,总存在x∈(-2,t),满足 ,并确定这样的x的个数.
,并确定这样的x的个数.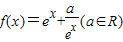 (其中e是自然对数的底数)
(其中e是自然对数的底数)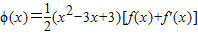 ,求证:对于任意的t>-2,总存在x∈(-2,t),满足
,求证:对于任意的t>-2,总存在x∈(-2,t),满足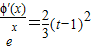 ,并确定这样的x的个数.
,并确定这样的x的个数.