题目内容
已知函数 ,判断下列三个命题的真假:
,判断下列三个命题的真假:
①f(x)<1;
②x=0为f(x)的一个极大值点;
③当x∈(0,2π)时,f(x)没有极值点.其中真命题的个数是
- A.0个
- B.1个
- C.2个
- D.3个
B
分析:对于①针对函数 的性质,只须考虑当0<x<
的性质,只须考虑当0<x< 时的函数值即可,再利用单位圆中的三角函数线,通过面积关系证明sinx<x;
时的函数值即可,再利用单位圆中的三角函数线,通过面积关系证明sinx<x;
对于②③,利用商的导数运算法则及基本初等函数的导数公式,求出函数的导数 ,然后根据导函数的符号确定函数的单调性即可得到结论.
,然后根据导函数的符号确定函数的单调性即可得到结论.
解答:①针对函数 的性质,只须考虑当0<x<
的性质,只须考虑当0<x< 时的函数值即可,
时的函数值即可,
如图,在单位圆中,有sinx=MA,
连接AN,则S△OAN<S扇形OAN,
设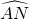 的长为l,则x=
的长为l,则x=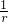 =1,
=1,
∴ ON•MA<
ON•MA< ON•x,即MA<x,
ON•x,即MA<x,
又sinx=MA,
∴sinx<x,∴ ,故①正确;
,故①正确;
②因为x为0时分母无意义,所以x=0不能为f(x)的一个极大值点,故②错误;
③由于函数的导数 ,
,
当x 时,xcosx-sinx<0,即f'(x)<0,
时,xcosx-sinx<0,即f'(x)<0,
当 时,xcosx-sinx>0,即f'(x)>0,则函数在
时,xcosx-sinx>0,即f'(x)>0,则函数在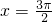 时取得极值,故③错误.
时取得极值,故③错误.
故答案选 B.
点评:本题考查的知识点是,判断命题真假,比较综合的考查了三角函数、导数的一些性质,我们可以根据三角函数和导数的常用结论对三个结论逐一进行判断,可以得到正确的结论.
分析:对于①针对函数
 的性质,只须考虑当0<x<
的性质,只须考虑当0<x< 时的函数值即可,再利用单位圆中的三角函数线,通过面积关系证明sinx<x;
时的函数值即可,再利用单位圆中的三角函数线,通过面积关系证明sinx<x; 对于②③,利用商的导数运算法则及基本初等函数的导数公式,求出函数的导数
 ,然后根据导函数的符号确定函数的单调性即可得到结论.
,然后根据导函数的符号确定函数的单调性即可得到结论.解答:①针对函数
 的性质,只须考虑当0<x<
的性质,只须考虑当0<x< 时的函数值即可,
时的函数值即可,如图,在单位圆中,有sinx=MA,

连接AN,则S△OAN<S扇形OAN,
设
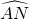 的长为l,则x=
的长为l,则x=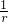 =1,
=1,∴
 ON•MA<
ON•MA< ON•x,即MA<x,
ON•x,即MA<x,又sinx=MA,
∴sinx<x,∴
 ,故①正确;
,故①正确;②因为x为0时分母无意义,所以x=0不能为f(x)的一个极大值点,故②错误;
③由于函数的导数
 ,
,当x
 时,xcosx-sinx<0,即f'(x)<0,
时,xcosx-sinx<0,即f'(x)<0,当
 时,xcosx-sinx>0,即f'(x)>0,则函数在
时,xcosx-sinx>0,即f'(x)>0,则函数在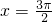 时取得极值,故③错误.
时取得极值,故③错误.故答案选 B.
点评:本题考查的知识点是,判断命题真假,比较综合的考查了三角函数、导数的一些性质,我们可以根据三角函数和导数的常用结论对三个结论逐一进行判断,可以得到正确的结论.

练习册系列答案
相关题目
 ,给出下列三个判断:①函数f(x)的最小正周期为π;②函数f(x)在区间
,给出下列三个判断:①函数f(x)的最小正周期为π;②函数f(x)在区间 内是增函数;③函数f(x)关于点
内是增函数;③函数f(x)关于点 对称.以上三个判断中正确的个数为( )
对称.以上三个判断中正确的个数为( ) ,给出下列三个判断:①函数f(x)的最小正周期为π;②函数f(x)在区间
,给出下列三个判断:①函数f(x)的最小正周期为π;②函数f(x)在区间 内是增函数;③函数f(x)关于点
内是增函数;③函数f(x)关于点 对称.以上三个判断中正确的个数为( )
对称.以上三个判断中正确的个数为( ) ,判断下列三个命题的真假:
,判断下列三个命题的真假: