题目内容
12.已知函数f(x)=|x+a2|+|x-a-1|.(1)证明:f(x)≥$\frac{3}{4}$;
(2)若f(4)<13,求实数a的取值范围.
分析 (1)利用绝对值不等式,结合配方法,即可证明结论;
(2)f(4)<13,可得$\left\{\begin{array}{l}{a≥3}\\{{a}^{2}+a+1<13}\end{array}\right.$或$\left\{\begin{array}{l}{a<3}\\{{a}^{2}-a+7<13}\end{array}\right.$,即可求实数a的取值范围.
解答 (1)证明:f(x)=|x+a2|+|x-a-1|≥|x+a2-(x-a-1)|=|a2+a+1|=$(a+\frac{1}{2})^{2}$+$\frac{3}{4}$≥$\frac{3}{4}$.
(2)解:f(4)=$\left\{\begin{array}{l}{{a}^{2}+a+1,a≥3}\\{{a}^{2}-a+7,a<3}\end{array}\right.$,
∵f(4)<13,
∴$\left\{\begin{array}{l}{a≥3}\\{{a}^{2}+a+1<13}\end{array}\right.$或$\left\{\begin{array}{l}{a<3}\\{{a}^{2}-a+7<13}\end{array}\right.$,
∴-2<a<3.
点评 本题考查不等式的证明,考查不等式的解法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
3.设复数Z1,Z2在复平面内的对应点关于虚轴对称,Z1(1-i)=3-i,则Z2=( )
| A. | 2+i | B. | 2-i | C. | -2+i | D. | -2-i |
20.已知函数f(x)=ex-ax有两个零点x1,x2,x1<x2,则下面说法正确的是( )
| A. | x1+x2<2 | B. | a<e | ||
| C. | x1x2>1 | D. | 有极小值点x0,且x1+x2<2x0 |
7.已知各项均为整数的数列{an}中,a1=2,且对任意的n∈N*,满足an+1-an<2n+$\frac{1}{2},{a_{n+2}}-{a_n}>3×{2^n}$-1,则a2017=22017.
17.已知A,B是单位圆上的两点,O为圆心,且∠AOB=90°,MN是圆O的一条直径,点C在圆内,且满足$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+(1-λ)$\overrightarrow{OB}$(λ∈R),则$\overrightarrow{CM}$•$\overrightarrow{CN}$的最小值为( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{3}{4}$ | D. | -1 |
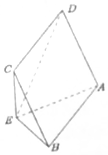 如图,在几何体ABCDE中,ABCD为正方形,CE⊥平面ABE,且异面直线AD、CE所成的角为30°.
如图,在几何体ABCDE中,ABCD为正方形,CE⊥平面ABE,且异面直线AD、CE所成的角为30°.