题目内容
在数列{an}中 ,且
,且
(1)求a3、a4,并求出数列{an}的通项公式;
(2)设
 ,求证:对?n∈N*,都有b1+b2+…bn
,求证:对?n∈N*,都有b1+b2+…bn .
.
【答案】分析:(1)利用数列递推式,计算a3、a4,猜想通项,利用数学归纳法证明数列{an}的通项公式;
(2)利用裂项法求和,再用分析法进行证明.
解答:(1)解:∵ ,
,
∴a3= ,a4=
,a4= ,
,
猜想 ,利用数学归纳法证明如下:
,利用数学归纳法证明如下:
①显然当n=1,2,3,4时,结论成立;
②假设当n=k(k≥3)时,结论成立,即
则n=k+1时, =
= =
= =
=
∴n=k+1时,结论成立
综上, ;
;
(2)证明: =
= (
( )
)
∴b1+b2+…+bn= [(
[( )+(
)+( -
- )+…+(
)+…+( )]=
)]= (
( )
)
要证b1+b2+…bn ,只需证明
,只需证明 (
( )
)
即证
即证3n+2-2 <3n-1
<3n-1
即证 ,显然成立
,显然成立
∴b1+b2+…+bn .
.
点评:本题考查数列递推式,考查数列的通项与求和,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.
(2)利用裂项法求和,再用分析法进行证明.
解答:(1)解:∵
 ,
,
∴a3=
 ,a4=
,a4= ,
,猜想
 ,利用数学归纳法证明如下:
,利用数学归纳法证明如下:①显然当n=1,2,3,4时,结论成立;
②假设当n=k(k≥3)时,结论成立,即

则n=k+1时,
 =
= =
= =
=
∴n=k+1时,结论成立
综上,
 ;
;(2)证明:
 =
= (
( )
)∴b1+b2+…+bn=
 [(
[( )+(
)+( -
- )+…+(
)+…+( )]=
)]= (
( )
)要证b1+b2+…bn
 ,只需证明
,只需证明 (
( )
)
即证

即证3n+2-2
 <3n-1
<3n-1即证
 ,显然成立
,显然成立∴b1+b2+…+bn
 .
.点评:本题考查数列递推式,考查数列的通项与求和,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 ,且
,且
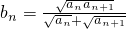 ,求证:对?n∈N*,都有b1+b2+…bn
,求证:对?n∈N*,都有b1+b2+…bn .
. 且满足an+1-2an+1=0
且满足an+1-2an+1=0 .
. 且c∈R)”是“{an}是等比数列”的( )
且c∈R)”是“{an}是等比数列”的( ) ,且Sn=9,则n= .
,且Sn=9,则n= .