题目内容
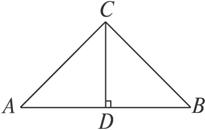
 如图,△ABC是某屋顶的断面,CD⊥AB,横梁AB的长是竖梁CD长的2倍.设计时应使y=tanA+2tanB保持最小,试确定D点的位置,并求y的最小值.
如图,△ABC是某屋顶的断面,CD⊥AB,横梁AB的长是竖梁CD长的2倍.设计时应使y=tanA+2tanB保持最小,试确定D点的位置,并求y的最小值.分析:首先设CD=1,则AB=2,再设AD=x,得BD=2-x,(0<x<2),然后根据直角三角形中三角函数的定义,得到tanA=
且tgB=
,代入y=tanA+2tanB的表达式,再进行配凑,得到y=-
,最后通过基本不等式讨论分母的最小值,可得y的最小值是
.根据取等号的条件得到:当且仅当x=2
-2时,取到这个最小值,求出AD与DB的比值,从而确定D点的位置,问题得到解决.
| 1 |
| x |
| 1 |
| 2-x |
| 1 | ||
x+2+
|
3+2
| ||
| 2 |
| 2 |
解答:解:设CD=1,则AB=2,再设AD=x,得BD=2-x,(0<x<2)
∵Rt△ACD中,tanA=
=
,Rt△BCD中,tanB=
=
∴y=tanA+2tanB=
+
=
+
=
=
=-
∵x+2+
≥4
;当且仅当(x+2)2=8,x=2
-2时取等号
∴当x=2
-2时,y取得最小值-
=
此时DB=2-(2
-2)=4-2
,
∴AD:DB=
=
答:取AD:DB=1:
时,y有最小值
∵Rt△ACD中,tanA=
| CD |
| AD |
| 1 |
| x |
| CD |
| BD |
| 1 |
| 2-x |
∴y=tanA+2tanB=
| CD |
| AD |
| 2CD |
| BD |
=
| 1 |
| x |
| 2 |
| 2-x |
| x+2 |
| x(2-x) |
| 1 | ||
|
| 1 | ||
x+2+
|
∵x+2+
| 8 |
| x+2 |
| 2 |
| 2 |
∴当x=2
| 2 |
| 1 | ||
4
|
3+2
| ||
| 2 |
此时DB=2-(2
| 2 |
| 2 |
∴AD:DB=
2
| ||
4-2
|
| 1 | ||
|
答:取AD:DB=1:
| 2 |
3+2
| ||
| 2 |
点评:本题借助于一个实际问题,通过求函数的最小值,着重考查了任意角三角函数的定义、基本不等式和函数的值域与最值等知识点,属于中档题.

练习册系列答案
相关题目
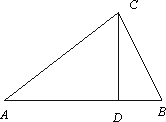
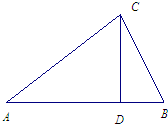 如图,△ABC是某屋顶的断面,CD⊥AB,横梁AB的长是竖梁CD长的2倍.设计时应使y=tanA+2tanB保持最小,试确定D点的位置,并求y的最小值.
如图,△ABC是某屋顶的断面,CD⊥AB,横梁AB的长是竖梁CD长的2倍.设计时应使y=tanA+2tanB保持最小,试确定D点的位置,并求y的最小值.