题目内容
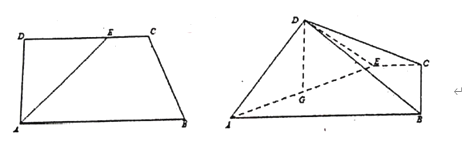
【题目】如下面左图,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 折起,得到四棱锥
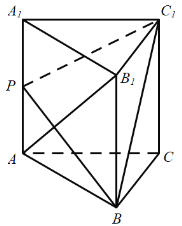
折起,得到四棱锥![]() (如下面右图).
(如下面右图).
(1)求四棱锥![]() 的体积的最大值;
的体积的最大值;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]()
【解析】
(1)当平面![]()
![]() 平面
平面![]() 时,体积最大;根据已知条件,求得底面面积和棱锥的高,即可求得体积的最大值;
时,体积最大;根据已知条件,求得底面面积和棱锥的高,即可求得体积的最大值;
(2)构造与平面![]() 平行的平面,即可容易求得点
平行的平面,即可容易求得点![]() 所在位置.
所在位置.
(1)由题意,要使得四棱锥![]() 的体积最大,就要使平面
的体积最大,就要使平面![]()
![]() 平面
平面![]() .
.
设![]() 为
为![]() 中点,连接
中点,连接![]() .如下图所示:
.如下图所示:

![]() ,
,![]() ,
,
![]() 平面
平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]()
![]() .
.![]()
![]() 平面
平面![]() .
.
![]() 平面
平面![]()
![]() ,则
,则![]() ,
,![]()
![]() 四棱锥
四棱锥![]() 的体积的最大值为
的体积的最大值为![]()
![]() .
.
(2)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,则
,则![]() ,
,
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]()


又![]() ,
,![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]()
![]() ,
,![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]()
又![]() ,
,![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]()
所以在![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]() .
.

练习册系列答案
相关题目
【题目】第十三届全国人大常委会第十一次会议审议的《固体废物污染环境防治法(修订草案)》中,提出推行生活垃圾分类制度,这是生活垃圾分类首次被纳入国家立法中.为了解某城市居民的垃圾分类意识与政府相关法规宣传普及的关系,对某试点社区抽取![]() 户居民进行调查,得到如下的
户居民进行调查,得到如下的![]() 列联表.
列联表.
分类意识强 | 分类意识弱 | 合计 | |
试点后 |
| ||
试点前 |
| ||
合计 |
|
已知在抽取的![]() 户居民中随机抽取
户居民中随机抽取![]() 户,抽到分类意识强的概率为
户,抽到分类意识强的概率为![]() .
.
(1)请将上面的![]() 列联表补充完整;
列联表补充完整;
(2)判断是否有![]() 的把握认为居民分类意识的强弱与政府宣传普及工作有关?说明你的理由;
的把握认为居民分类意识的强弱与政府宣传普及工作有关?说明你的理由;
参考公式: ,其中
,其中![]() .
.
下面的临界值表仅供参考
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|