题目内容
12.已知角α的顶点与原点重合,始边与x轴的非负半轴重合,终边过点P(sin$\frac{π}{8}$,cos$\frac{π}{8}$ ),则sin(2α-$\frac{π}{12}$)=$\frac{\sqrt{3}}{2}$.分析 由三角函数定义和二倍角公式可得sin2α,cos2α,sin$\frac{π}{12}$,cos$\frac{π}{12}$的值,代入两角差的正弦公式计算可得.
解答 解:由题意和三角函数的定义可得cosα=sin$\frac{π}{8}$,sinα=cos$\frac{π}{8}$,
∴sin2α=2sinαcosα=2sin$\frac{π}{8}$cos$\frac{π}{8}$=sin$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$,
∴cos2α=cos2α-sin2α=sin2$\frac{π}{8}$-cos2$\frac{π}{8}$=-cos$\frac{π}{4}$=-$\frac{\sqrt{2}}{2}$,
∴sin$\frac{π}{12}$=$\sqrt{\frac{1-cos\frac{π}{6}}{2}}$=$\frac{\sqrt{6}-\sqrt{2}}{4}$,
cos$\frac{π}{12}$=$\sqrt{\frac{1+cos\frac{π}{6}}{2}}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
∴sin(2α-$\frac{π}{12}$)=sin2αcos$\frac{π}{12}$-cos2αsin$\frac{π}{12}$
=$\frac{\sqrt{2}}{2}×\frac{\sqrt{6}+\sqrt{2}}{4}$-(-$\frac{\sqrt{2}}{2}$)×$\frac{\sqrt{6}-\sqrt{2}}{4}$=$\frac{\sqrt{3}}{2}$
故答案为:$\frac{\sqrt{3}}{2}$
点评 本题考查两角和与差的三角函数公式,涉及二倍角公式,属中档题.

| A. | 2 | B. | -1 | C. | 1 | D. | ±1 |
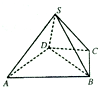 如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.
如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.