题目内容
如图是某直三棱柱被削去上底后的直观图与三视图的侧视图和俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示:
(1)求出该几何体的体积;
(2)求证:EM∥平面ABC.

(1)求出该几何体的体积;
(2)求证:EM∥平面ABC.

分析:(1)由侧视图是直角梯形,俯视图是等腰直角三角形,得四棱锥的高为2,求出底面梯形的面积,代入体积公式计算;
(2)取BC的中点O,连接OA,OE,证明四边形AOME为平行四边形,可得EM∥AO,再由线面平行的判定定理证明EM∥平面ABC.
(2)取BC的中点O,连接OA,OE,证明四边形AOME为平行四边形,可得EM∥AO,再由线面平行的判定定理证明EM∥平面ABC.
解答: 解:(1)侧视图是直角梯形,俯视图是等腰直角三角形,
解:(1)侧视图是直角梯形,俯视图是等腰直角三角形,
根据三视图的数据,四棱锥的高为2,
∴几何体的体积V=
×
×2×2=4;
(2)连接EM,取BC的中点O,连接OA,OE,
∵O、M分别是BC,BD的中点,∴OM∥CD,OM=
CD,
由侧视图知AE=
CD,AE∥CD,∴OM∥AE,OM=AE,
∴四边形AOME为平行四边形,∴EM∥AO,AO?平面ABC,EM?平面ABC,
∴EM∥平面ABC.
 解:(1)侧视图是直角梯形,俯视图是等腰直角三角形,
解:(1)侧视图是直角梯形,俯视图是等腰直角三角形,根据三视图的数据,四棱锥的高为2,
∴几何体的体积V=
| 1 |
| 3 |
| 2+4 |
| 2 |
(2)连接EM,取BC的中点O,连接OA,OE,
∵O、M分别是BC,BD的中点,∴OM∥CD,OM=
| 1 |
| 2 |
由侧视图知AE=
| 1 |
| 2 |
∴四边形AOME为平行四边形,∴EM∥AO,AO?平面ABC,EM?平面ABC,
∴EM∥平面ABC.
点评:本题考查了根据三视图的数据求几何体的体积,考查了线面平行的证明,解题的关键是判断三视图的数据所对应的几何量.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
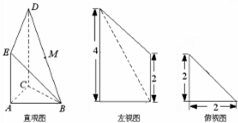 (2012•上饶一模)如图是某直三棱柱被削去上底后的直观图与三视图的左视图、俯视图,在直观图中,M是BD的中点,左视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(2012•上饶一模)如图是某直三棱柱被削去上底后的直观图与三视图的左视图、俯视图,在直观图中,M是BD的中点,左视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.

