题目内容
如图是某直三棱柱被削去上底后所得几何体的直观图、左视图、俯视图,左视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示,
(1)求该几何体的表面积及体积;
(2)求异面直线AC,BD所成的角的余弦值.

(1)求该几何体的表面积及体积;
(2)求异面直线AC,BD所成的角的余弦值.

分析:(1)由几何体的直观图与左视图、俯视图判断几何体各面的形状,利用左视图与俯视图给出的数据求各面的面积,再求和可得几何体的表面积;判断四棱锥的高于底面,利用棱锥的体积公式计算可求其体积.
(2)建立空间直角坐标系,给出相关点A、C、B,D的坐标,求出向量
,
的坐标,利用向量坐标运算求向量夹角的余弦值.
(2)建立空间直角坐标系,给出相关点A、C、B,D的坐标,求出向量
| CA |
| BD |
解答: 解:(1)由左视图知四棱锥的底面为直角梯形,AE=2,CD=4,BC=2,∴SACDE=
解:(1)由左视图知四棱锥的底面为直角梯形,AE=2,CD=4,BC=2,∴SACDE=
×2=6
由俯视图知△ABC为等腰直角三角形,∴S△ABC=
×2×2=2;
侧面△BCD为直角三角形,S△BCD=
×4×2=4;
侧面△ABE为直角三角形,AB=2
,∴S△ABE=
×2×2
=2
;
BE=
=
=2
,DE=
=2
,BD=2
∵BE2+DE2=BD2,△BDE为直角三角形,∴S△BDE=
×2
×2
=2
,
∴几何体的表面积为S=12+2
+2
;
由几何体的左视图与俯视图知:BC为四棱锥的高,且BC=2,
∴VB-ACDE=
×6×2=4.
(2)以C为原点,CA为x轴,CB为y轴,CD为z轴建立空间直角坐标系,
则C(0,0,0),A(2,0,0),B(0,2,0),D(0,0,4),
=(2,0,0),
=(0,-2,4),
cos<
,
>=
=
=
,
∴异面直线AC,BD所成的角的余弦值为
.
 解:(1)由左视图知四棱锥的底面为直角梯形,AE=2,CD=4,BC=2,∴SACDE=
解:(1)由左视图知四棱锥的底面为直角梯形,AE=2,CD=4,BC=2,∴SACDE=| 4+2 |
| 2 |
由俯视图知△ABC为等腰直角三角形,∴S△ABC=
| 1 |
| 2 |
侧面△BCD为直角三角形,S△BCD=
| 1 |
| 2 |
侧面△ABE为直角三角形,AB=2
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
BE=
| AB2+AE2 |
| 4+8 |
| 3 |
| 4+4 |
| 2 |
| 5 |
∵BE2+DE2=BD2,△BDE为直角三角形,∴S△BDE=
| 1 |
| 2 |
| 3 |
| 2 |
| 6 |
∴几何体的表面积为S=12+2
| 2 |
| 6 |
由几何体的左视图与俯视图知:BC为四棱锥的高,且BC=2,
∴VB-ACDE=
| 1 |
| 3 |
(2)以C为原点,CA为x轴,CB为y轴,CD为z轴建立空间直角坐标系,
则C(0,0,0),A(2,0,0),B(0,2,0),D(0,0,4),
| CA |
| BD |
cos<
| CA |
| BD |
| ||||
|
|
| 4 | ||
2×2
|
| ||
| 5 |
∴异面直线AC,BD所成的角的余弦值为
| ||
| 5 |
点评:本题考查了由三视图求几何体的表面积与体积,考查了用向量坐标运算求异面直线所成角的余弦值,正确运用三视图的数据是解答本题的关键.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
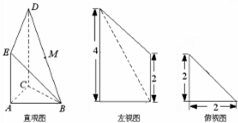 (2012•上饶一模)如图是某直三棱柱被削去上底后的直观图与三视图的左视图、俯视图,在直观图中,M是BD的中点,左视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(2012•上饶一模)如图是某直三棱柱被削去上底后的直观图与三视图的左视图、俯视图,在直观图中,M是BD的中点,左视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.

