题目内容
设数列{an}是等差数列，其中am=a，an=b，am+n=
，用类比的思想方法，在等比数列{bn}中，若bm=a，bn=b，写出
| b•n-a•m |
| n-m |
b•(
)
| a |
| b |
| n |
| n-m |
b•(
)
．| a |
| b |
| n |
| n-m |
分析：由m＜n，bn=b1•qn-1=a，bm=b1•qm-1=b，知qn-m=
，q=(
)
，所以bm+n=bm•qn=b•qn=b•[（
）
]n=b•(
)
．
| a |
| b |
| a |
| b |
| 1 |
| n-m |
| a |
| b |
| 1 |
| n-m |
| a |
| b |
| n |
| n-m |
解答：解：m＜n，bm=a，bn=b，
bn=b1•qn-1=a，
bm=b1•qm-1=b，
∴qn-m=
，
q=(
)
，
∴bm+n=bm•qn=b•qn
=b•[（
）
]n
=b•(
)
．
故答案为：b•(
)
．
bn=b1•qn-1=a，
bm=b1•qm-1=b，
∴qn-m=
| a |
| b |
q=(
| a |
| b |
| 1 |
| n-m |
∴bm+n=bm•qn=b•qn
=b•[（
| a |
| b |
| 1 |
| n-m |
=b•(
| a |
| b |
| n |
| n-m |
故答案为：b•(
| a |
| b |
| n |
| n-m |
点评：本题考查数列的性质和应用，解题时要注意等比数列前n项和公式和通项公式的合理运用．
练习册系列答案
相关题目
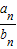}的前n项和Sn．
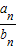}的前n项和Sn．
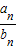}的前n项和Sn．