题目内容
【题目】在等腰三角形ABC中，∠A=150°，AB=AC=1，则 
=（ ）
A.
B.
C.
D.
【答案】A
【解析】解：方法一：如图所示，过点C作CD⊥BA，交于点D， ∴ 
=﹣ 
=﹣| || |cosB=﹣[| |+| 
|cos（180°﹣150°）]=﹣（1+ 
）=﹣1﹣
方法二，等腰三角形ABC中，∠A=150°，AB=AC=1，
∴B=15°，
∴cos15°=cos（45°﹣30°）= 
× + × 
= 
由余弦定理可得BC2=AB2+AC2﹣2ABACcosA=1+1﹣2×（﹣ ）=2+ 
，
∴BC= 
∴ =| 
|| |cos（180°﹣15°）=1× ×（﹣ ）=﹣1﹣
故选：A．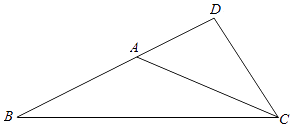
练习册系列答案
相关题目
