题目内容
已知实数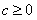 ,曲线
,曲线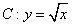 与直线
与直线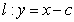 的交点为
的交点为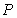 (异于原点
(异于原点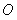 ),在曲线
),在曲线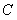 上取一点
上取一点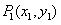 ,过点
,过点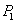 作
作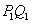 平行于
平行于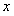 轴,交直线
轴,交直线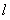 于点
于点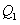 ,过点
,过点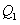 作
作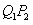 平行于
平行于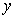 轴,交曲线
轴,交曲线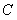 于点
于点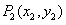 ,接着过点
,接着过点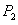 作
作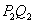 平行于
平行于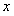 轴,交直线
轴,交直线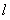 于点
于点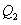 ,过点
,过点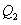 作
作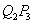 平行于
平行于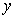 轴,交曲线
轴,交曲线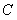 于点
于点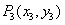 ,如此下去,可以得到点
,如此下去,可以得到点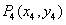 ,
,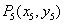 ,…,
,…,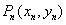 ,… . 设点
,… . 设点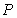 的坐标为
的坐标为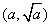 ,
,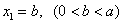 .
.
(Ⅰ)试用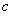 表示
表示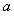 ,并证明
,并证明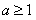 ;
;
(Ⅱ)试证明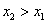 ,且
,且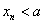 (
(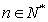 );
);
(Ⅲ)当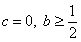 时,求证:
时,求证: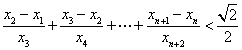 (
(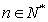 ).
).
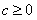 ,曲线
,曲线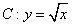 与直线
与直线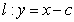 的交点为
的交点为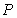 (异于原点
(异于原点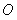 ),在曲线
),在曲线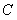 上取一点
上取一点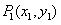 ,过点
,过点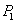 作
作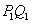 平行于
平行于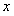 轴,交直线
轴,交直线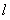 于点
于点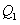 ,过点
,过点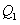 作
作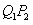 平行于
平行于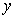 轴,交曲线
轴,交曲线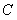 于点
于点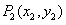 ,接着过点
,接着过点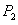 作
作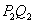 平行于
平行于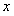 轴,交直线
轴,交直线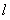 于点
于点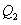 ,过点
,过点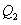 作
作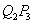 平行于
平行于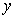 轴,交曲线
轴,交曲线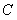 于点
于点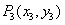 ,如此下去,可以得到点
,如此下去,可以得到点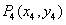 ,
,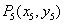 ,…,
,…,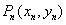 ,… . 设点
,… . 设点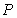 的坐标为
的坐标为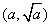 ,
,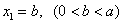 .
.(Ⅰ)试用
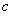 表示
表示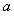 ,并证明
,并证明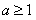 ;
; (Ⅱ)试证明
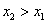 ,且
,且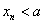 (
(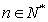 );
);(Ⅲ)当
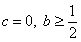 时,求证:
时,求证: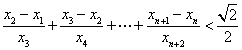 (
(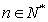 ).
).见解析部分
(Ⅰ)点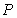 的坐标
的坐标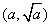 满足方程组
满足方程组 ,所以
,所以 ,
,
解得: ,故
,故 ,
,
因为 ,所以故
,所以故 ,故
,故 .
.
(Ⅱ)由已知 ,
, ,
, ,
,
即: ,
,
所以
因为 ,所以
,所以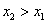 .
.
下面用数学归纳法证明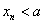 (
(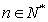 )
)
○11当 时,
时, 成立;
成立;
○22假设当 时,有
时,有 成立,(
成立,( )
)
则当 时,
时,
所以
所以当 时命题也成立,
时命题也成立,
综上所述由○11,○22知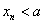 (
(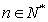 )成立.
)成立.
(注:此问答题如:只是由图可知,而不作严格证明,得分一律不超过2分)
(Ⅲ)当 时,
时, ,
, (
( ),
),
所以 .
.
因为 ,所以当
,所以当 时,由(Ⅱ)知
时,由(Ⅱ)知 ,
,
所以有 .
.
又因为 ,
, 
所以 ,
, ,
,
故有:

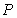 的坐标
的坐标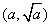 满足方程组
满足方程组 ,所以
,所以 ,
, 解得:
 ,故
,故 ,
,因为
 ,所以故
,所以故 ,故
,故 .
.(Ⅱ)由已知
 ,
, ,
, ,
,即:
 ,
, 所以

因为
 ,所以
,所以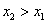 .
. 下面用数学归纳法证明
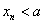 (
(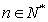 )
)○11当
 时,
时, 成立;
成立;○22假设当
 时,有
时,有 成立,(
成立,( )
)则当
 时,
时,
所以

所以当
 时命题也成立,
时命题也成立,综上所述由○11,○22知
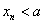 (
(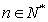 )成立.
)成立.(注:此问答题如:只是由图可知,而不作严格证明,得分一律不超过2分)
(Ⅲ)当
 时,
时, ,
, (
( ),
),所以
 .
.因为
 ,所以当
,所以当 时,由(Ⅱ)知
时,由(Ⅱ)知 ,
,所以有
 .
.又因为
 ,
, 
所以
 ,
, ,
,故有:


练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
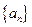 的各项均为正数,观察下面程序框图,当
的各项均为正数,观察下面程序框图,当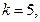
 时,分别
时,分别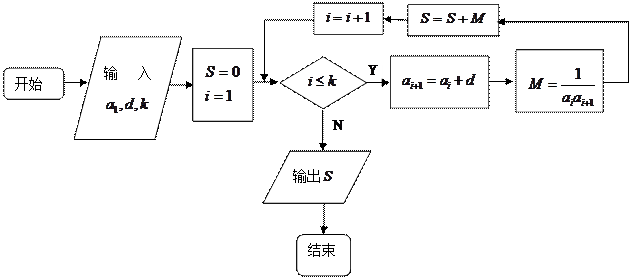
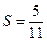 和
和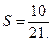 .
.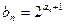 ,
,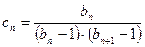
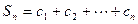 求证:
求证: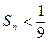 .
. ;(Ⅱ)求{an}前n项和Sn的最大值.
;(Ⅱ)求{an}前n项和Sn的最大值.




 项和.
项和. 及
及 满足
满足 求数列
求数列 .
.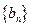 的前
的前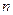 项和为
项和为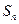 ,且
,且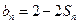 ;数列
;数列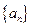 为等差数列,且
为等差数列,且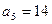 ,
,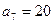 .(1)求数列
.(1)求数列 ,
,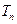 为数列
为数列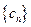 的前
的前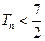 .
.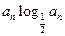 ,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立,试求m的取值范围。
,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立,试求m的取值范围。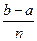
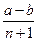

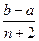
 北黄冈中学·
北黄冈中学·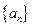 满足
满足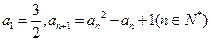 ,求
,求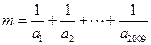 的
的 整数部分。
整数部分。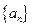 的前
的前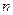 和为
和为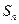 ,且有
,且有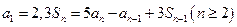
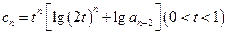 ,且数列
,且数列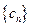 中的每一项总小于它后面的项,求实数
中的每一项总小于它后面的项,求实数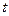 的取值范围。
的取值范围。