题目内容
定义在 上的函数
上的函数 满足:①
满足:① (
(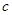 为正常数);②当
为正常数);②当 时,
时, .若函数的所有极大值点均在同一条直线上,则
.若函数的所有极大值点均在同一条直线上,则 _____________.
_____________.
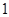 或
或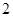 .
.
解析试题分析:当 时,
时, ,故函数
,故函数 在
在 上单调递增,在
上单调递增,在 上单调递增,故函数
上单调递增,故函数 在
在 处取得极大值
处取得极大值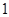 ,当
,当 时,则
时,则 ,此时
,此时 ,此时,函数
,此时,函数 在
在 处取得极大值
处取得极大值 ,对任意
,对任意 ,当
,当 时,函数
时,函数 在
在 处取得极大值
处取得极大值 ,故函数
,故函数 的所有极大值点为
的所有极大值点为 ,由于这些极大值点均在同一直线上,则直线
,由于这些极大值点均在同一直线上,则直线 的斜率为定值,即
的斜率为定值,即 为定值,故
为定值,故 或
或 ,即
,即 或
或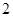 .
.
考点:1.函数的极值;2.直线的斜率

练习册系列答案
相关题目
 在区间
在区间 上是增函数,则实数
上是增函数,则实数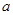 的取值范围是 .
的取值范围是 .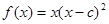 在
在 处有极小值,则实数
处有极小值,则实数 为 .
为 . 有六个不同的单调区间,则实数
有六个不同的单调区间,则实数 的取值范围是____________ .
的取值范围是____________ . 是定义域为
是定义域为 的奇函数,且
的奇函数,且 时,
时, ,则函数
,则函数 的图象在
的图象在 处的切线方程是
处的切线方程是 ,则
,则 .
. 的导函数在区间
的导函数在区间 上是增函数,则函数
上是增函数,则函数



 在点
在点 处的切线方程是 .
处的切线方程是 .