题目内容
已知函数f(x)=x+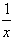 ,
,
(Ⅰ)判断函数的奇偶性,并加以证明;
(Ⅱ)用定义证明f(x)在(0,1)上是减函数;
(Ⅲ)函数f(x)在(-1,0)上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程)
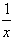 ,
,(Ⅰ)判断函数的奇偶性,并加以证明;
(Ⅱ)用定义证明f(x)在(0,1)上是减函数;
(Ⅲ)函数f(x)在(-1,0)上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程)
解:(Ⅰ)函数为奇函数, ;
;
(Ⅱ)设 ,
,
 ,
,
 ,
,
∴ ,
,
 ,
,
∴ ,
,
∴ ,
,
因此函数f(x)在(0,1)上是减函数;
(Ⅲ)f(x)在(-1,0)上是减函数。
 ;
;(Ⅱ)设
 ,
, ,
, ,
,∴
 ,
, ,
,∴
 ,
,∴
 ,
,因此函数f(x)在(0,1)上是减函数;
(Ⅲ)f(x)在(-1,0)上是减函数。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|