题目内容
【题目】设数列{an}的各项都为正数，其前n项和为Sn ， 已知4Sn=an2+2an ．
（1）求a1级数列{an}的通项公式；
（2）设数列{bn}前n项和为Tn ， 且bn= 
，若λTn＜n+（﹣1）n36对n∈N*恒成立，求实数λ的取值范围．
【答案】
（1）解：∵4Sn=an2+2an，
∴4Sn+1=an+12+2an+1，
两式相减得：4an+1=an+12+2an+1﹣（an2+2an），
整理得：（an+1+an）（an+1﹣an）=2（an+1+an），
又∵数列{an}的各项都为正数，
∴an+1﹣an=2，
又∵4a1= 
+2a1，
∴a1=2或a1=0（舍），
∴数列{an}的通项公式an=2n
（2）解：bn= 
= 
= 
= 
﹣ 
，
∴Tn=1﹣ 
+ ﹣ 
+…+ ﹣ =1﹣ = 
，
∵λTn＜n+（﹣1）n36对n∈N*恒成立，
∴λ＜ 
=n+1+（﹣1）n 
对n∈N*恒成立，
记f（n）=n+1+（﹣1）n ，
当n为偶数时，f（n）=n+1+
=37+n+ 
≥37+2 
=37+26=49，
当且仅当n= 即n=6时取等号；
当n为奇数时，f（n）=n+1﹣
=n﹣ ﹣35
≥1﹣ 
﹣35=﹣70；
综上所述，实数λ的取值范围为：（﹣∞，﹣70）
【解析】（1）利用4Sn=an2+2an与4Sn+1=an+12+2an+1作差、整理得an+1﹣an=2，进而计算可得结论；（2）通过裂项、并项相加可知Tn= ，进而问题转化为求f（n）=n+1+（﹣1）n 的最小值，通过对n分奇数、偶数两种情况讨论即可．
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系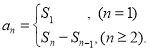
；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能正确解答此题．
