题目内容
设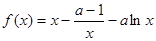
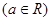 .
.
(1)若 是函数
是函数 的极大值点,求
的极大值点,求 的取值范围;
的取值范围;
(2)当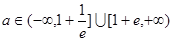 时,若在
时,若在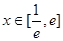 上至少存在一点
上至少存在一点 ,使
,使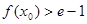 成立,求
成立,求 的取值范围.
的取值范围.
(1)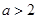 ; (2)
; (2) 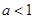 .
.
解析试题分析:(1)对函数求导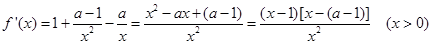 ,
,
求出零点,分析单调性,找出极大值点与1的关系,进行计算;
(2)原问题转化为当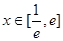 时,
时, 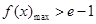 ,利用第一问求出最值,解不等式.
,利用第一问求出最值,解不等式.
试题解析:(1)
当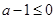 时,f(x)在(0,1)递减,在(1,+
时,f(x)在(0,1)递减,在(1,+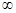 )递增,故f(x)在x=1处取到极小值,不合舍去。
)递增,故f(x)在x=1处取到极小值,不合舍去。
当 时,f(x)在(0,a-1)递增,在(a-1,1)递减,在(1,+
时,f(x)在(0,a-1)递增,在(a-1,1)递减,在(1,+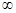 )递增,故f(x)在x=1处取到极小值,不合舍去。
)递增,故f(x)在x=1处取到极小值,不合舍去。
当 时,f(x)在(0,1)和(1,+
时,f(x)在(0,1)和(1,+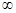 )均递增,故f(x)在x=1处没有极值,不合舍去。
)均递增,故f(x)在x=1处没有极值,不合舍去。
当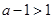 时,f(x)在(0,1)递增,在(1,a-1)递减,在(a-1, +
时,f(x)在(0,1)递增,在(1,a-1)递减,在(a-1, +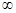 )递增,故f(x)在x=1处取到极大值,符合题意。
)递增,故f(x)在x=1处取到极大值,符合题意。
综上所述,当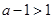 ,即
,即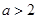 时,
时, 是函数
是函数 的极大值点. 6分
的极大值点. 6分
(2)在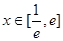 上至少存在一点
上至少存在一点 ,使
,使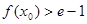 成立,等价于
成立,等价于
当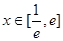 时,
时, 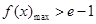 .由(1)知,①当
.由(1)知,①当 ,即
,即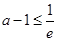 时,
时,
函数 在
在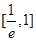 上递减,在
上递减,在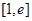 上递增,
上递增,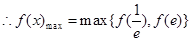 .
.
由 ,解得
,解得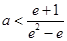 .由
.由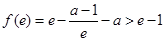 ,解得
,解得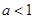
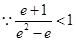 ,
, 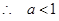 ; ②当
; ②当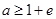 ,即
,即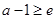 时,函数
时,函数 在
在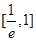 上递增,在
上递增,在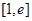 上递减,
上递减, .
.
综上所述,当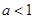 时,在
时,在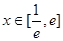 上至少存在一点
上至少存在一点 ,使
,使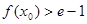 成立. 13分
成立. 13分
考点:导数计算,转化与化归思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
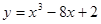
 处的的切线方程;
处的的切线方程;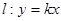 ,求切线方程.
,求切线方程. .
.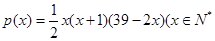 ,且
,且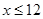 )。该商品第x月的进货单价q(x)(单位:元)与x的近似关系是
)。该商品第x月的进货单价q(x)(单位:元)与x的近似关系是
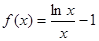 .
.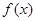 的单调性;
的单调性;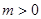 ,求
,求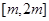 上的最大值;
上的最大值;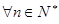 ,不等式
,不等式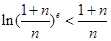 .
.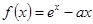 (
(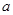 为常数)的图像与
为常数)的图像与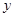 轴交于点
轴交于点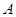 ,曲线
,曲线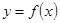 在点
在点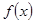 的极值;(2)证明:当
的极值;(2)证明:当 时,
时,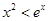 ;
;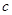 ,总存在
,总存在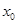 ,使得当
,使得当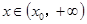 ,恒有
,恒有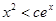 .
. ,
,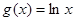 .
. 的极值;(2)若
的极值;(2)若 恒成立,求实数
恒成立,求实数 的值;
的值;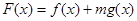
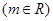 有两个极值点
有两个极值点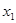 、
、 (
(
 的取值范围,并证明
的取值范围,并证明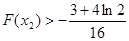 .
. 在区间
在区间 上恰有一个极值点,则实数
上恰有一个极值点,则实数 的取值范围是
的取值范围是  在
在 上的最大值与最小值的差为 .
上的最大值与最小值的差为 .