Question

3．已知函数f（x）=$\left\{\begin{array}{l}{|{2}^{x}-1|（x＜1）}\\{-（x-2）^{2}+1（x≥1）}\end{array}\right.$，则关于x的方程f（x+$\frac{1}{x}$-1）=a的实根个数最多为（　　）

• A． 5个
• B． 6个
• C． 7个
• D． 8个

Answer 1

分析 将x+$\frac{1}{x}$-1视为一个整体，利用换元的思想方法和已知中函数f（x）=$\left\{\begin{array}{l}{|{2}^{x}-1|（x＜1）}\\{-（x-2）^{2}+1（x≥1）}\end{array}\right.$，结合二次函数，指数函数的图象和性质，及函数图象的对折变换，分类讨论，可得答案．

解答 解：令t=x+$\frac{1}{x}$-1，则t∈（-∞，-3]∪[1，+∞），
画出函数f（x）=$\left\{\begin{array}{l}{|{2}^{x}-1|（x＜1）}\\{-（x-2）^{2}+1（x≥1）}\end{array}\right.$，x∈（-∞，-3]∪[1，+∞）时的图象如下图所示：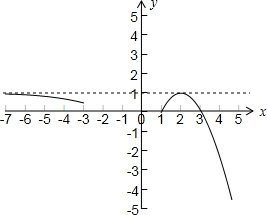
，
由图可知：当a∈[$\frac{7}{8}$，1）时，关于x的方程f（x）=a的实根个数最多为3个，
故关于x的方程f（x+$\frac{1}{x}$-1）=a的实根个数最多为6个，
故选：B．

点评 本题重点考查了分段函数、函数的零点等知识，属于中档题．