题目内容
11.已知点P(0,5)及圆C:x2+y2+4x-12y+24=0(1)写出圆C的圆心坐标及半径;
(2)若直线l过点P且被圆C截得的线段长为4$\sqrt{3}$,求l的方程;
(3)过点P的圆C的弦的中点D的轨迹方程.
分析 (1)整理出圆C的标准方程,确定圆的圆心与半径;
(2)分类讨论,利用直线ι被圆C截得的线段长为4$\sqrt{3}$,可得直线ι与圆心的距离为2,由此可得结论;
(3)设过P点的圆c的弦的中点D的坐标为(x,y),利用CD⊥PD,可得方程.
解答 解:(1)整理圆的方程得(x+2)2+(y-6)2=16,
圆心(-2,6),半径r=4;(3分)
(2)由圆C:x2+y2+4x-12y+24=0得圆心坐标为(-2,6),半径为4
又∵直线ι被圆C截得的线段长为4$\sqrt{3}$,∴直线ι与圆心的距离为2,
当直线斜率存在时,设L的斜率是k,过P(0,5),设直线ι:y=kx+5,即kx-y+5=0;
∵直线ι与圆C的圆心相距为2,∴d=$\frac{||-2k-6+5|}{\sqrt{{k}^{2}+1}}$=2,解得k=$\frac{3}{4}$,此时直线的方程为3x-4y+20=0;
当直线的斜率不存在时,直线的方程为x=0,也符合题意.
故所求直线的方程为3x-4y+20=0或x=0.(8分)
(3)设过P点的圆c的弦的中点D的坐标为(x,y),则
∵CD⊥PD,∴(x+2)•x+(y-6)•(y-5)=0
化简得所求轨迹方程为x2+y2+2x-11y+30=0.(14分)
点评 本题考查圆的方程,考查直线与圆的位置关系,考查轨迹方程,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
1.设AB为半圆O的直径,点C是弧AB的一个三等份点,点D是直径AB的一个三等份点,且点C、D均靠近B点,若半圆O的半径为3,则$\overrightarrow{DC}•\overrightarrow{AB}$=( )
| A. | 0 | B. | $\frac{3}{2}$ | C. | 3 | D. | $\frac{9}{2}\sqrt{3}$ |
6.已知具有线性相关的两个变量x,y之间的一组数据如下:
且回归方程是$\widehat{y}$=bx+a,其中b=0.95,则当x=6时,y的预测值为( )
| x | 0 | 1 | 2 | 3 | 4 |
| y | 2.2 | 4.3 | 4.5 | 4.8 | 6.7 |
| A. | 8.1 | B. | 8.2 | C. | 8.3 | D. | 8.4 |
16.运行如图的程序框图,则输出s的结果是( )
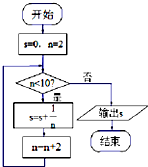

| A. | $\frac{25}{24}$ | B. | $\frac{1}{6}$ | C. | $\frac{3}{4}$ | D. | $\frac{11}{12}$ |
3.已知函数f(x)=$\left\{\begin{array}{l}{|{2}^{x}-1|(x<1)}\\{-(x-2)^{2}+1(x≥1)}\end{array}\right.$,则关于x的方程f(x+$\frac{1}{x}$-1)=a的实根个数最多为( )
| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
20.已知函数f(x)=ln(1-$\frac{a}{x+1}$)(a∈R),命题p:?a∈R,f(x)是奇函数,命题q:?a∈R,f(x)在定义域内是增函数,那么下列命题是真命题的是( )
| A. | ¬p | B. | p∧q | C. | (¬p)∧q | D. | p∧(¬q) |