题目内容
如图,四棱锥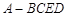 的底面
的底面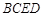 是直角梯形,
是直角梯形,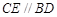 ,
,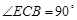 ,
,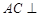 平面
平面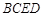 ,
,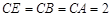 ,
,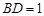 .
.
(1)求直线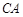 与平面
与平面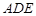 所成角的正弦值;
所成角的正弦值;
(2)在线段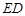 上是否存在一点
上是否存在一点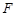 ,使得异面直线
,使得异面直线 与
与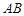 所成角余 弦值等
所成角余 弦值等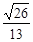 ?若存在,试确定点
?若存在,试确定点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.

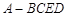 的底面
的底面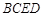 是直角梯形,
是直角梯形,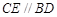 ,
,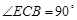 ,
,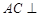 平面
平面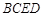 ,
,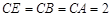 ,
,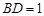 .
.(1)求直线
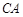 与平面
与平面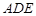 所成角的正弦值;
所成角的正弦值;(2)在线段
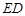 上是否存在一点
上是否存在一点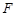 ,使得异面直线
,使得异面直线 与
与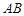 所成角余 弦值等
所成角余 弦值等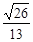 ?若存在,试确定点
?若存在,试确定点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(I)如图建立空间直角坐标系.则A(2,0,0),
B(0,2,0),D(0,2,1),E(0,0,2).
 ,
, ,
,
设平面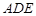 的法向量是
的法向量是 ,
,
∴ ,取
,取 ,得
,得 , …………(4分)
, …………(4分)

(II)假设存在 ,使得
,使得 ,则
,则 ,
,
∴ ,∵
,∵ ,∴
,∴

∴当 是线段
是线段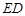 的中点时,异面直线
的中点时,异面直线 与
与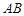 所成角余弦值等
所成角余弦值等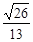 .
.

B(0,2,0),D(0,2,1),E(0,0,2).
 ,
, ,
,
设平面
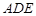 的法向量是
的法向量是 ,
, ∴
 ,取
,取 ,得
,得 , …………(4分)
, …………(4分)
(II)假设存在
 ,使得
,使得 ,则
,则 ,
,∴
 ,∵
,∵ ,∴
,∴

∴当
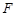 是线段
是线段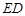 的中点时,异面直线
的中点时,异面直线 与
与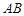 所成角余弦值等
所成角余弦值等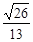 .
.
略

练习册系列答案
相关题目
 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD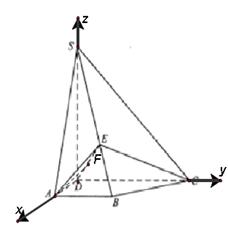
 的大小为
的大小为 ,且
,且 ,则异面直线m,n所成的角为( )
,则异面直线m,n所成的角为( ) B
B  C
C  D
D 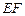 ⊥平面
⊥平面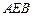 ,
, 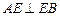 ,
,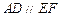 ,
,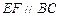 ,
,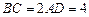 ,
,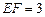 ,
,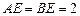 ,
,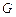 是
是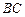 的中点.
的中点.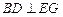 ;
;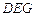 与平面
与平面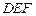 所成锐二面角的余弦值.
所成锐二面角的余弦值.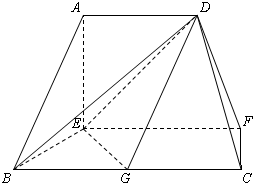
 中,
中, ,
, ,
, 为线段
为线段 上一动点,现将
上一动点,现将 沿
沿 折起,使点
折起,使点 在面
在面 上的射影
上的射影 在直线
在直线 ,则
,则
 中,已知
中,已知 在棱
在棱 上,且
上,且 ,若
,若 与平面
与平面 所成的角为
所成的角为 ,则
,则
