题目内容
（2008•宝山区一模）已知正四棱柱ABCD-A1B1C1D1底面边长是1，体积是2，M、N分别是棱BB1、B1C1的中点，求异面直线MN与AC所成角的大小．（结果用反三角函数值表示）分析：连接AD1，AC，CD1 由 MN∥AD1，可知∠D1AC （或其补角）即为异面直线MN与AC所成角的平面角．在△D1AC中求解即可．
解答：解：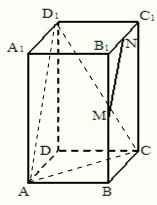
连接AD1，AC，CD1∵MN∥AD1，∴∠D1AC （或其补角）即为异面直线MN与AC所成角的平面角．
由已知，AA1=2，在△D1AC中，AC2=2，AD12=CD12=5，由余弦定理得cos∠D1AC=
=
∴∠D1AC=arccos
，
异面直线MN与AC所成角的大小=arccos
，
连接AD1，AC，CD1∵MN∥AD1，∴∠D1AC （或其补角）即为异面直线MN与AC所成角的平面角．由已知，AA1=2，在△D1AC中，AC2=2，AD12=CD12=5，由余弦定理得cos∠D1AC=
| 5+2-5 | ||||
2×
|
| ||
| 10 |
| ||
| 10 |
异面直线MN与AC所成角的大小=arccos
| ||
| 10 |
点评：本题考查异面直线夹角的计算，考查空间想象能力，转化能力、计算能力．
练习册系列答案
相关题目
（2008•宝山区一模）如图，已知正△A1B1C1的边长是1，面积是P1，取△A1B1C1各边的中点A2，B2，C2，△A2B2C2的面积为P2，再取△A2B2C2各边的中点A3，B3，C3，△A3B3C3的面积为P3，依此类推．记Sn=P1+P2+…+Pn，则
（2008•宝山区一模）如果执行下面的程序框图，那么输出的S=
（2008•宝山区一模）函数是这样定义的：对于任意整数m，当实数x满足不等式