题目内容
对于连续函数f(x)和g(x),函数|f(x)-g(x)|在闭区间[a,b]上的最大值称为f(x)与g(x)在闭区间[a,b]上的“绝对差”,记为△(f(x),g(x)),则x∈[2,3]时,△( ,
, x2-x)=________.
x2-x)=________.
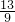
分析:由已知中关于f(x)与g(x)在闭区间[a,b]上的“绝对差”的定义,我们构造函数F(x)=f(x)-g(x)=
 -(
-( x2-x),根据函数的值域,及分析出F(x)>0恒成立,再根据x∈[2,3]时,F′(x)<0,可得当x=2时F(x)=f(x)-g(x)取最大值,代入计算即可得到答案.
x2-x),根据函数的值域,及分析出F(x)>0恒成立,再根据x∈[2,3]时,F′(x)<0,可得当x=2时F(x)=f(x)-g(x)取最大值,代入计算即可得到答案.解答:令F(x)=f(x)-g(x)=
 -(
-( x2-x)
x2-x)∴x∈[2,3]时,F(x)>0恒成立
又∵x∈[2,3]时,F′(x)<0
∴x∈[2,3]时,F(x)为减函数
当x=2时F(x)=f(x)-g(x)的最大值为
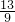
∴△(
 ,
, x2-x)=
x2-x)=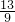
故答案为:
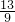 .
.点评:本题考查的知识点是函数最值的应用,其中根据y=
 与y=
与y= x2-x的值域,分析出x∈[2,3]时,F(x)>0恒成立,从而避免讨论绝对值问题是解答本题的关键.
x2-x的值域,分析出x∈[2,3]时,F(x)>0恒成立,从而避免讨论绝对值问题是解答本题的关键. 
练习册系列答案
相关题目
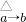 (f(x),g(x)).若
(f(x),g(x)).若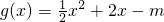 ,且
,且 (f(x),g(x))=
(f(x),g(x))= ,求m的值.
,求m的值.