Question

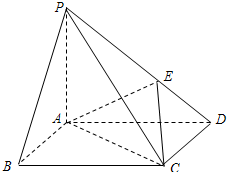如图，在底面是正方形的四棱锥P-ABCD中，PA=AB=1，PB=PD=

2

，点E在PD上，且PE：ED=2：1．
（1）求证：PA⊥平面ABCD；
（2）求二面角D-AC-E的余弦值；
（3）在棱PC上是否存在一点F，使得BF∥平面ACE．

Answer 1

分析：（1）PA=AB=1，PB=

2

，可得PA⊥AB．同理PA⊥AD．得证．
（2）设出平面ACE的一个法向量为

n

，根据法向量与平面内任一向量垂直，数量积为0，构造方程组，求出平面ACE的法向量为

n

的坐标，代入面面夹角向量公式，即可求出答案．
（3）假设在棱PC存在一点F，使得BF∥平面AEC，则须

BF

与

n

垂直．数量积为0，利用方程解的存在与否判定点F是否存在．

解答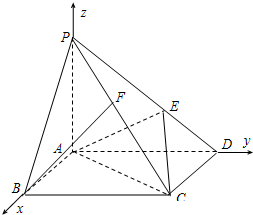：解：（1）正方形ABCD边长为1，PA=1，PB=PD=

2

，
所以，∠PAB=∠PAD=90°，即PA⊥AB，PA⊥AD，AB∩AD=A，
根据直线和平面垂直的判定定理，
有PA⊥平面ABCD．         
（2）如图，以A为坐标原点，直线AB、AD、AP分别x轴、y轴、z轴，建立空间直角坐标系．
则

AC

=(1 ，1 ，0)，

AE

=(0 ，

2

3

 ，

1

3

)，
由（1）知

AP

为平面ACD的法向量，

AP

=(0 ，0 ，1)，
设平面ACE的法向量为

n

=(a，b，c)，
则

a+b=0 2 3 b+ 1 3 c=0

令c=6，则b=-3，a=3，

n

=(3，-3，6)，…（4分）
设二面角D-AC-E的平面角为θ，则|cosθ|=

| n • AP |

| n || AP |

=

6

3

，
又有图可知，θ为锐角，
故所求二面角的余弦值为

6

3

．
（3）设

PF

=λ

PC

(λ∈[0 ， 1])，则

PF

=λ(1 ，  1，-1)=(λ，  λ，-λ)，

BF

=

BP

+

PF

=(λ-1，  λ，1-λ)，
若BF∥平面ACE，则

BF

⊥

n

，即

BF

•

n

=0，（λ-1，λ，1-λ）•（3，-3，6）=0，
计算得λ=

1

2

所以，存在满足题意的点，即当F是棱PC的中点时，BF∥平面ACE．…（8分）

点评：（1）注意勾股定理及其逆定理在证明线线垂直时价值．
（2）两平面法向量的夹角θ与两平面间的夹角φ关系是相等或互补．但必有|cosθ|=|cosφ|．
（3）此问重点考查了利用空间向量的方法及假设存在于方程的思想进行求解的方法