题目内容
19.如果实数x,y满足条件$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-2≥0}\\{2x-y-2≤0}\end{array}\right.$,则z=$\frac{x}{y}$的最大值为2.分析 由约束条件作出可行域,由z=$\frac{x}{y}$的几何意义,即可行域内的动点与坐标原点连线的斜率的倒数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-2≥0}\\{2x-y-2≤0}\end{array}\right.$作出可行域,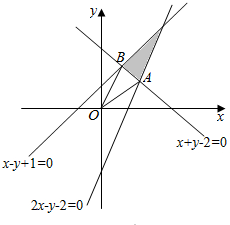
联立$\left\{\begin{array}{l}{2x-y-2=0}\\{x+y-2=0}\end{array}\right.$,解得A($\frac{4}{3},\frac{2}{3}$),
联立$\left\{\begin{array}{l}{x-y+1=0}\\{x+y-2=0}\end{array}\right.$,解得B($\frac{1}{2},\frac{3}{2}$),
∴${k}_{OA}=\frac{\frac{2}{3}}{\frac{4}{3}}=\frac{1}{2}$,${k}_{OB}=\frac{\frac{3}{2}}{\frac{1}{2}}=3$,
∴z=$\frac{x}{y}$∈[$\frac{1}{3}$,2].
则z=$\frac{x}{y}$的最大值为2.
故答案为:2.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
9.已知圆C1:x2+y2+2x+8y-8=0与圆C2:(x-2)2+(y-2)2=10相交于A,B两点,则弦长|AB|=( )
| A. | 10 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 4$\sqrt{5}$ |
14.对变量x,y有观测数据(xi,yi)(i=1,2,3,4,5),得表1;对变量u,v有观测数据(ui,vi)(i=1,2,3,4,5),得表2.由这两个表可以判断( )
表1:
表2:
表1:
| x | 1 | 2 | 3 | 4 | 5 |
| y | 2.9 | 3.3 | 3.6 | 4.4 | 5.1 |
| u | 1 | 2 | 3 | 4 | 5 |
| v | 25 | 20 | 21 | 15 | 13 |
| A. | 变量x与y正相关,u与v正相关 | B. | 变量x与y负相关,u与v正相关 | ||
| C. | 变量x与y负相关,u与v负相关 | D. | 变量x与y正相关,u与v负相关 |
11.为了得到函数y=cos(2x-$\frac{2π}{3}$),x∈R的图象,只要把函数y=cos2x,x∈R的图象( )
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{2π}{3}$个单位 |