题目内容
执行如图所示的程序框图,若输入如下四个函数: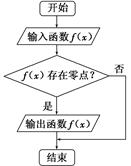
①y=2x;②y=-2x;③f(x)=x+x-1;④f(x)=x-x-1.
则输出函数的序号为________.
(4)
解析试题分析:含条件结构的程序框图,可以先分析给出的四个函数的零点情况,判断哪个函数满足条件,若函数有零点,则输出f(x)结束循环,无零点的函数则不输出.函数f(x)=2x定义域为R,值域为(0,+∞),图象与x轴无交点,函数无零点;
函数f(x)=-2x的图象与f(x)=2x的图象关于x轴对称,值域为(-∞,0),图象也与x轴无交点,函数无零点;
函数f(x)=x+x-1的定义域为{x|x≠0},当x>0时,f(x)=x+
 =2,
=2,
又函数f(x)为奇函数,所以当x<0时,f(x)≤-2,所以函数的值域为(-∞,-2)(2,+∞),所以函数无零点;
由x-x-1=0,得x? 解得x=-1,或x=1,所以函数有两个零点.
解得x=-1,或x=1,所以函数有两个零点.
综上,若输入的函数是①、②、③,则程序结束,只有输入④,算法输出序号为④的函数.
故选D.
考点:读程序框图能力,判断四个函数的零点情况

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数 的图象在点
的图象在点 处的切线
处的切线 被圆
被圆 所截得的弦长是
所截得的弦长是 ,则
,则
A. | B. | C. | D. |
已知过曲线 上一点P,原点为O,直线PO的倾斜角为
上一点P,原点为O,直线PO的倾斜角为 ,则P点坐标是( )
,则P点坐标是( )
| A.(3,4) | B. | C.(-3,-4) | D. |
如果输入 ,那么执行下图中算法后的输出结果是( )
,那么执行下图中算法后的输出结果是( )
A. | B. | C. | D. |
若圆x2+y2=4上每个点的横坐标不变.纵坐标缩短为原来的 ,则所得曲线的方程是( )
,则所得曲线的方程是( )
A. | B. | C. | D. |
 的通项公式为
的通项公式为 ,对于任意自然数
,对于任意自然数 都是递增数列,
都是递增数列, 的取值范围为 .
的取值范围为 . ,沿着较短的对角线
,沿着较短的对角线 对折,使得
对折,使得 ,
,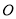 为
为 的中点.若P为AC上的点,且满足
的中点.若P为AC上的点,且满足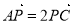 。
。
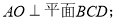
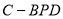 的体积;
的体积; 的余弦值.
的余弦值. ,则
,则 ”的逆命题为真
”的逆命题为真 为真”是“命题
为真”是“命题 为真”的必要不充分条件
为真”的必要不充分条件 ,均有
,均有 ”的否定是:“
”的否定是:“ ,使
,使 ”
” ,则( )
,则( ) B.
B.
 D.
D.