题目内容
7.已知以点$C(t,\frac{2}{t})(t∈R且t≠0)$为圆心的圆经过原点O,且与x轴交于点A,与y轴交于点B.(1)求证:△AOB的面积为定值.
(2)设直线2x+y-4=0与圆C交于点M,N,若|OM|=|ON|,求圆C的方程.
(3)当t>0时,在(2)的条件下,设P,Q分别是直线l:x+y+2=0和圆C上的动点,求|PB|+|PQ|的最小值及此时点P的坐标.
分析 (1)推导出圆的方程为x2-2tx+y2-$\frac{4}{t}y$=0.与坐标轴的交点分别为:A(2t,0),B(0,$\frac{4}{t}$).由此能证明S△OAB=4,为定值.
(2)由|OM|=|ON|,得原点O在线段MN的垂直平分线上,设线段MN的中点为H,则C,H,O三点共线,从而求出t=±2,由此能求出圆C的方程.
(3)圆心C(2,1),半径r=$\sqrt{5}$,点B(0,2)关于直线x+y+2=0的对称点为B′(-4,-2),则|PB|+|PQ|=|PB′|+|PQ|≥|B′Q|,由此能求出|PB|+|PQ|的最小值和点P坐标.
解答 证明:(1)由题意可得:圆的方程为:(x-t)2+(y-$\frac{2}{t}$)2=t2+$\frac{4}{{t}^{2}}$,化为:x2-2tx+y2-$\frac{4}{t}y$=0.
与坐标轴的交点分别为:A(2t,0),B(0,$\frac{4}{t}$).
∴S△OAB=$\frac{1}{2}×|2t|×|\frac{4}{t}|$=4,为定值.
解:(2)∵|OM|=|ON|,∴原点O在线段MN的垂直平分线上,设线段MN的中点为H,
则C,H,O三点共线,
OC的斜率k=$\frac{\frac{2}{t}}{t}$=$\frac{2}{{t}^{2}}$,∴$\frac{2}{{t}^{2}}$×(-2)=-1,解得t=±2,
可得圆心C(2,1),或(-2,-1).
∴圆C的方程为:(x-2)2+(y-1)2=5,或(x+2)2+(y+1)2=5.
(3)由(2)可知:圆心C(2,1),半径r=$\sqrt{5}$,点B(0,2)关于直线x+y+2=0的对称点为B′(-4,-2),
则|PB|+|PQ|=|PB′|+|PQ|≥|B′Q|,
又点B′到圆上点Q的最短距离为|B′C|-r=$\sqrt{(-6)^{2}+(-3)^{2}}$-$\sqrt{5}$=2$\sqrt{5}$,
则|PB|+|PQ|的最小值为2$\sqrt{5}$.
直线B′C的方程为:y=$\frac{1}{2}$x,此时点P为直线B′C与直线l的交点,
故所求的点P(-$\frac{4}{3}$,-$\frac{2}{3}$).
点评 本题考查三角形面积为定值的证明,考查圆的方程的求法,考查两线段落和的最小值及点的坐标的求法,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”其意思为:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈,上棱长2丈,无宽,高1丈.现给出该楔体的三视图,其中网格纸上小正方形的边长为1丈,则该楔体的体积为( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”其意思为:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈,上棱长2丈,无宽,高1丈.现给出该楔体的三视图,其中网格纸上小正方形的边长为1丈,则该楔体的体积为( )| A. | 4立方丈 | B. | 5立方丈 | C. | 6立方丈 | D. | 8立方丈 |
| A. | 3 | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | 2 |
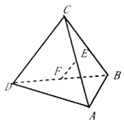 已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=6,CD=10,EF=7,则AB与CD所成角的度数为( )
已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=6,CD=10,EF=7,则AB与CD所成角的度数为( )| A. | 120° | B. | 45° | C. | 60° | D. | 90° |