题目内容
(本小题8分)设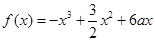 .
.
(1)当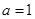 时,求
时,求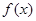 在区间
在区间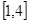 上的最值;
上的最值;
(2)若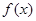 在
在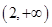 上存在单调递增区间,求
上存在单调递增区间,求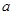 的取值范围.
的取值范围.
【答案】
(1) ,
, ;(2)
;(2) .
.
【解析】本试题主要是考查了导数在研究函数中的运用。利用导数的符号与函数单调性的关系,求解函数在给定区间的最值问题,以及关于函数的单调区间,求解参数的取值范围的逆向解题。
(1)首先根据a=1,求解析式,然后求解导数,令导数大于零或者小于零,得到单调性,进而确定最值。
(2)因为函数 在
在 上存在单调递增区间,即导函数在
上存在单调递增区间,即导函数在 上存在函数值大于零的部分,说明不等式有解可知。
上存在函数值大于零的部分,说明不等式有解可知。
解:已知 ,
, ,
,
(1)已知 ,
,

 在
在 上递增,在
上递增,在 上递减
上递减
 ,
, ,
,
 ,
, ………5分
………5分
(2)函数 在
在 上存在单调递增区间,即导函数在
上存在单调递增区间,即导函数在 上存在函数值大于零的部分,
上存在函数值大于零的部分, ………8分
………8分

练习册系列答案
相关题目
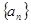 的前
的前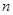 项和为
项和为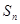 ,已知
,已知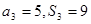 ,
,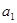 和公差
和公差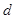 的值;
的值;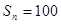 ,求
,求 (常数
(常数
 的定义域;
的定义域; 满足什么条件时,
满足什么条件时, 在
在 上恒取正值。
上恒取正值。 ,政府补贴为
,政府补贴为 。根据市场调查,当
。根据市场调查,当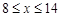 时,淡水鱼的市场日供应量
时,淡水鱼的市场日供应量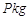 与市场日需求量
与市场日需求量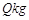 近似满足关系:
近似满足关系: ,
,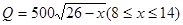 ;当
;当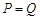 时的市场价格称为市场平衡价格。
时的市场价格称为市场平衡价格。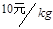 ,政府需要补贴吗?如果需要,至少为多少
,政府需要补贴吗?如果需要,至少为多少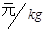 ?
? 的前
的前 项和为
项和为 ,点
,点 在直线
在直线 上;数列
上;数列 满足
满足 ,且
,且 ,它的前9项和为153.
,它的前9项和为153. ,求数列
,求数列 的前
的前 .
.