题目内容
正四面体的各顶点为A1,A2,A3,A4,进入某顶点的动点X不停留在同一个顶点上,每隔1秒钟向其他三个顶点以相同的概率移动.n秒后X在Ai(i=1,2,3,4)的概率用Pi(n)(n=0,1,2…)表示.当P1(0)=| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 8 |
(1)求P2(1),P2(2);
(2)求P2(n)与P2(n-1)的关系(n∈N*)及P2(n)关于n的表达式,P1(n)关于n的表达式.
分析:(1)P2(1)即1秒后动点在A2的概率,它有三种情况:开始时(0秒)在A1,1秒后移动到A2;开始时在A3,1秒后移动到A2;开始时在A4,1秒后移动到A2.根据这三种结果互斥得到结论.
(2)n秒后动点在A2,即n-1秒后动点不在A2,其概率为1-P2(n-1),得到概率之间的关系是数列递推关系,从概率问题自然地过渡到数列问题,再用数列的办法解决.
(2)n秒后动点在A2,即n-1秒后动点不在A2,其概率为1-P2(n-1),得到概率之间的关系是数列递推关系,从概率问题自然地过渡到数列问题,再用数列的办法解决.
解答:解:(1)P2(1)即1秒后动点在A2的概率,它有三种情况;
①开始时(0秒)在A1,1秒后移动到A2;
由题意知,每隔1秒钟动点X从一个顶点移动到另一个顶点的概率均为
;
所以这种情况的概率为:P1(0)×
=
;
②开始时在A3,1秒后移动到A2;其概率为:P3(0)×
=
;
③开始时在A4,1秒后移动到A2;其概率为:P4(0)×
=
;
又这三种情况互斥,
∴P2(1)=
+
+
=
.
我们设想一下,如果仍然按这个办法计算P2(2),
将不胜其烦,因为首先要算P1(1)、P3(1)、P4(1);
事实上1秒后动点在A2,即开始时(0秒)动点不在A2,其概率为:1-P2(0)=
,
而每隔1秒钟动点X从一个顶点移动到另一个顶点的概率均为
;
所以P2(1)=
×
=
.类似的,2秒后动点在A2,
即1秒后动点不在A2,其概率为:1-P2(1)=
,
∴P2(2)=
×
=
;
(2)n秒后动点在A2,即n-1秒后动点不在A2,
其概率为:1-P2(n-1),
∴P2(n)=[1-P2(n-1)]×
.
至此,问题化归为数列问题.即:已知数列{P2(n)}满足:
P2(n)=-
P2(n-1)+
,求通项公式.
用待定系数法构造等比数列,
设P2(n)+x=-
[P2(n-1)+x],得x=-
,可见
数列{P2(n)-
}是以-
为公比的等比数列,其首项为P2(1)-
=-
∴P2(n)-
=-
(-
)n-1,P2(n)=
-
(-
)n-1.
完全类似地,可得P1(n)=-
P1(n-1)+
,于是有P1(n)-
=-
[P1(n-1)-
]
但P1(1)-
=0,
∴数列{P1(n)}是常数列,即P1(n)=
.
①开始时(0秒)在A1,1秒后移动到A2;
由题意知,每隔1秒钟动点X从一个顶点移动到另一个顶点的概率均为
| 1 |
| 3 |
所以这种情况的概率为:P1(0)×
| 1 |
| 3 |
| 1 |
| 12 |
②开始时在A3,1秒后移动到A2;其概率为:P3(0)×
| 1 |
| 3 |
| 1 |
| 24 |
③开始时在A4,1秒后移动到A2;其概率为:P4(0)×
| 1 |
| 3 |
| 1 |
| 24 |
又这三种情况互斥,
∴P2(1)=
| 1 |
| 12 |
| 1 |
| 24 |
| 1 |
| 24 |
| 1 |
| 6 |
我们设想一下,如果仍然按这个办法计算P2(2),
将不胜其烦,因为首先要算P1(1)、P3(1)、P4(1);
事实上1秒后动点在A2,即开始时(0秒)动点不在A2,其概率为:1-P2(0)=
| 1 |
| 2 |
而每隔1秒钟动点X从一个顶点移动到另一个顶点的概率均为
| 1 |
| 3 |
所以P2(1)=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
即1秒后动点不在A2,其概率为:1-P2(1)=
| 5 |
| 6 |
∴P2(2)=
| 5 |
| 6 |
| 1 |
| 3 |
| 5 |
| 18 |
(2)n秒后动点在A2,即n-1秒后动点不在A2,
其概率为:1-P2(n-1),
∴P2(n)=[1-P2(n-1)]×
| 1 |
| 3 |
至此,问题化归为数列问题.即:已知数列{P2(n)}满足:
P2(n)=-
| 1 |
| 3 |
| 1 |
| 3 |
用待定系数法构造等比数列,
设P2(n)+x=-
| 1 |
| 3 |
| 1 |
| 4 |
数列{P2(n)-
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
∴P2(n)-
| 1 |
| 4 |
| 1 |
| 12 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
| 1 |
| 3 |
完全类似地,可得P1(n)=-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
但P1(1)-
| 1 |
| 4 |
∴数列{P1(n)}是常数列,即P1(n)=
| 1 |
| 4 |
点评:本题的关键是第n秒后动点在某一顶点即意味着第n-1秒后动点不在该顶点,由此反映的它们的概率之间的关系正是数列的前后项之间的关系即递推关系,于是从概率问题自然地过渡到数列问题,再用数列的办法解决之.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
将棱长为3的正四面体的各顶点截去四个棱长为1的小正四面体(使截面平行于底面),所得几何体的表面积为( )
A、7
| ||
B、6
| ||
C、3
| ||
D、9
|
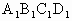 中,
中,


