题目内容
（本小题满分14分）
如图，在四棱锥P－ABCD中，PD⊥平面ABCD，四边形ABCD是菱形，AC＝6，BD＝8，E是PB上任意一点。
（1）求证：AC⊥DE；
（2）若PB与平面ABCD所成角为450，E是PB上的中点。
求三棱锥P－AED的体积．
如图，在四棱锥P－ABCD中，PD⊥平面ABCD，四边形ABCD是菱形，AC＝6，BD＝8，E是PB上任意一点。
（1）求证：AC⊥DE；
（2）若PB与平面ABCD所成角为450，E是PB上的中点。
求三棱锥P－AED的体积．
（1）证明：连接BD，设AC与BD相交于点F．
因为四边形ABCD是菱形，所以AC⊥BD． 2分
又因为PD⊥平面ABCD，AC
平面ABCD，所以PD⊥AC． 4分
而AC∩BD＝F，所以AC⊥平面PDB．
E为PB上任意一点，DE平面PBD，所以AC⊥DE． 7分
（2）由（1）知
平面
，
14分
因为四边形ABCD是菱形，所以AC⊥BD． 2分
又因为PD⊥平面ABCD，AC
平面ABCD，所以PD⊥AC． 4分而AC∩BD＝F，所以AC⊥平面PDB．
E为PB上任意一点，DE
平面PBD，所以AC⊥DE． 7分（2）由（1）知
平面， 14分略
练习册系列答案
相关题目
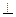平面ABC，BD//AE，且AC=AB=BC=AE=1，BD=2，F为CD中点。
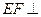平面BCD；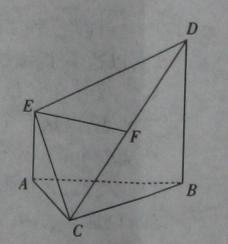
，过圆心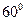
二面角的平面β截该球面得圆
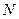.若该球面的半径为4，圆
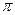，则圆
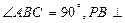平面ABC，AB=BC=2
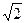，PB=2，则点B到平面PAC的距离是 
于同一平面的两平面互相平行；