题目内容
设y=f(x)为定义在区间I上的函数,若对I上任意两个实数x1,x2都有f(
)≤
[f(x1)+f(x2)]成立,则f(x)称为I上的凹函数.
(1)判断f(x)=
(x>0)是否为凹函数?
(2)已知函数f2(x)=x|ax-3|(a≠0)为区间[3,6]上的凹函数,请直接写出实数a的取值范围(不要求写出解题过程);
(3)设定义在R上的函数f3(x)满足对于任意实数x,y都有f3(x+y)=f3(x)•f3(y).求证:f3(x)为R上的凹函数.
| x1+x2 |
| 2 |
| 1 |
| 2 |
(1)判断f(x)=
| 3 |
| x |
(2)已知函数f2(x)=x|ax-3|(a≠0)为区间[3,6]上的凹函数,请直接写出实数a的取值范围(不要求写出解题过程);
(3)设定义在R上的函数f3(x)满足对于任意实数x,y都有f3(x+y)=f3(x)•f3(y).求证:f3(x)为R上的凹函数.
分析:(1)因为
[f(x1)+f(x2)]=
(
+
),所以利用均值定理即可得证
(2)利用凹函数的图象性质及函数f2(x)=x|ax-3|的图象特点,可得a的取值范围
(3)因为f3(x1)+f3(x2)=f3(
+
)+f3(
+
),利用已知抽象表达式,结合均值定理即可证明f3(x)为R上的凹函数
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| x1 |
| 3 |
| x2 |
(2)利用凹函数的图象性质及函数f2(x)=x|ax-3|的图象特点,可得a的取值范围
(3)因为f3(x1)+f3(x2)=f3(
| x1 |
| 2 |
| x1 |
| 2 |
| x2 |
| 2 |
| x2 |
| 2 |
解答:解:(1)f(x)是凹函数,证明如下:
?x1,x2∈(0,+∞),∵
[f(x1)+f(x2)]=
(
+
)≥
≥
=f(
)
∴f(
)≤
[f(x1)+f(x2)],
∴f(x)=
(x>0)是凹函数
(2)∵函数f2(x)=x|ax-3|=
结合二次函数的图象,要想使函数f2(x)为区间[3,6]上的凹函数,需a<0或
∴a的取值范围为(-∞,0)∪[1,+∞)
(3)证明:设?x1,x2∈R
f3(x1)+f3(x2)=f3(
+
)+f3(
+
)
=f32(
)+f32(
)≥2f3(
)•f3(
)=2f3(
)
即
≥f3(
)
故f3(x)为R上的凹函数
?x1,x2∈(0,+∞),∵
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| x1 |
| 3 |
| x2 |
| 3 | ||
|
| 3 | ||
|
| x1+x2 |
| 2 |
∴f(
| x1+x2 |
| 2 |
| 1 |
| 2 |
∴f(x)=
| 3 |
| x |
(2)∵函数f2(x)=x|ax-3|=
|
结合二次函数的图象,要想使函数f2(x)为区间[3,6]上的凹函数,需a<0或
|
∴a的取值范围为(-∞,0)∪[1,+∞)
(3)证明:设?x1,x2∈R
f3(x1)+f3(x2)=f3(
| x1 |
| 2 |
| x1 |
| 2 |
| x2 |
| 2 |
| x2 |
| 2 |
=f32(
| x1 |
| 2 |
| x2 |
| 2 |
| x1 |
| 2 |
| x2 |
| 2 |
| x1+x2 |
| 2 |
即
| f3(x1)+f3(x2) |
| 2 |
| x1+x2 |
| 2 |
故f3(x)为R上的凹函数
点评:本题考查了抽象函数表达式的意义和作用,代数变形和逻辑推理能力,数形结合的思想方法

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
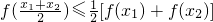 成立,则f(x)称为I上的凹函数.
成立,则f(x)称为I上的凹函数.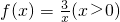 是否为凹函数?
是否为凹函数?