题目内容
8.已知两条直线m,n和两个平面α,β,下面给出四个命题中:①α∩β=m,n?α⇒m∥n或m与n相交;
②α∥β,m?α,n?β⇒m∥n;
③m∥n,m∥α⇒n∥α;
④α∩β=m,m∥n⇒n∥β且n∥α.其中正确命题的序号是①.
分析 根据空间线面位置关系的定义或判定定理进行分析.
解答 解:对于①,若α∩β=m,n?α,则m,n共面,故m与n平行或相交,故①正确;
对于②,若α∥β,m?α,n?β,则m,n没有公共点,故m与n平行或异面,故②错误;
对于③,若m∥n,m∥α,则n∥α或n?α,故③错误;
对于④,若α∩β=m,m∥n,则n∥α或n∥β,故④错误;
故答案为①.
点评 本题考查了空间线面位置关系的判断,属于中档题.

练习册系列答案
相关题目
18.若z(1+i)=2i则|z|等于( )
| A. | 3 | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | 2 |
19.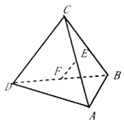 已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=6,CD=10,EF=7,则AB与CD所成角的度数为( )
已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=6,CD=10,EF=7,则AB与CD所成角的度数为( )
 已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=6,CD=10,EF=7,则AB与CD所成角的度数为( )
已知四面体ABCD中,E,F分别是AC,BD的中点,若AB=6,CD=10,EF=7,则AB与CD所成角的度数为( )| A. | 120° | B. | 45° | C. | 60° | D. | 90° |
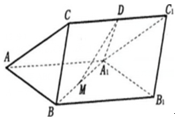 如图,三棱柱ABC-A1B1C1中,BC⊥平面ABB1A1,D,M分别为CC1和A1B的中点,△BA1B1是边长为2的正三角形,BC=1.
如图,三棱柱ABC-A1B1C1中,BC⊥平面ABB1A1,D,M分别为CC1和A1B的中点,△BA1B1是边长为2的正三角形,BC=1.