题目内容
(本小题满分13分)在 中,
中, ,
, .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 最大边的边长为
最大边的边长为 ,求最小边的边长.
,求最小边的边长.
(Ⅰ) .(Ⅱ)最小边
.(Ⅱ)最小边 .
.
解析试题分析:(I)根据 把tanA,tanB代入可求出tanC,再根据C的取值范围可求出C.
把tanA,tanB代入可求出tanC,再根据C的取值范围可求出C.
(II)由(I)可知AB边最大,tanA<tanB,从而可确定A最小,BC边最小,
因而根据三角函数的同角三角函数的基本关系式可得sinA,再根据正弦定理可求出BC边.
(Ⅰ) ,
, .
.
又 ,
, .
.
(Ⅱ) ,
, 边最大,即
边最大,即 .
.
又 ,
, 角
角 最小,
最小, 边为最小边.
边为最小边.
由 且
且 ,
,
得 .由
.由 得:
得: .
.
所以,最小边 .
.
考点:本小题主要考查了同角三角函数的基本关系式,两角和的正切公式.
点评:最大边的确定可以根据大角对大边原理,一般要要借助正切函数或正余弦函数的单调性确定A的大小,从而得到边的大小.

练习册系列答案
相关题目
△ABC的内角 的对边分别为
的对边分别为 ,若
,若 成等比数列,且
成等比数列,且 ,则
,则 ( )
( )
A. | B. | C.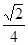 | D. |

 最小正周期及单调递增区间;
最小正周期及单调递增区间; 时,求
时,求 为锐角,
为锐角, ,
, ,求
,求 的值.
的值. ,
, 、b、c,且
、b、c,且 ,若向量
,若向量 共线,求
共线,求 .
. 的最小正周期及
的最小正周期及 ,且
,且 ,求
,求 的值.
的值. (2)
(2) .
. 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,
, ,且
,且
 与
与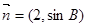 共线,求
共线,求 中,角
中,角 的对边分别为
的对边分别为 .
. ;
; ,且
,且 ,求
,求 .
.