题目内容
已知点M(-1,0),直线l:y=x+1与曲线C:
(α为参数)相交于P1,P2两点,
(1)求|MP1||MP2|;
(2)求|P1P2|.
|
(1)求|MP1||MP2|;
(2)求|P1P2|.
考点:参数方程化成普通方程
专题:计算题,坐标系和参数方程
分析:(1)将曲线C化为普通方程,直线l化为参数方程,将直线方程代入曲线C整理成关于t的二次方程,运用韦达定理,即可求出|MP1||MP2|;
(2)|P1P2|=|t1-t2|=
代入数据即可求得.
(2)|P1P2|=|t1-t2|=
| (t1+t2)2-4t1t2 |
解答:
解(1)曲线C:
(α为参数)的一般方程为:
+y2=1,
直线l:y=x+1的参数方程为:
(t为参数).
把直线方程
,代入曲线C,得:5t2-2
t-6=0,
设t1,t2是方程的两根,则t1+t2=
,t1t2=-
.
则|MP1||MP2|=|t1t2|=
;
(2)|P1P2|=|t1-t2|=
=
=
.
|
| x2 |
| 4 |
直线l:y=x+1的参数方程为:
|
把直线方程
|
| 2 |
设t1,t2是方程的两根,则t1+t2=
2
| ||
| 5 |
| 6 |
| 5 |
则|MP1||MP2|=|t1t2|=
| 6 |
| 5 |
(2)|P1P2|=|t1-t2|=
| (t1+t2)2-4t1t2 |
|
8
| ||
| 5 |
点评:本题考查参数方程与普通方程的互化,考查直线的参数方程的几何意义及运用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
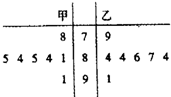 为迎接2013年全运会在注著名的海滨城市大连举行了场奥运选拔赛,其中甲乙两名运动员为争取最好一个参赛名额进行了7轮比赛的得分如茎叶图所示.
为迎接2013年全运会在注著名的海滨城市大连举行了场奥运选拔赛,其中甲乙两名运动员为争取最好一个参赛名额进行了7轮比赛的得分如茎叶图所示.